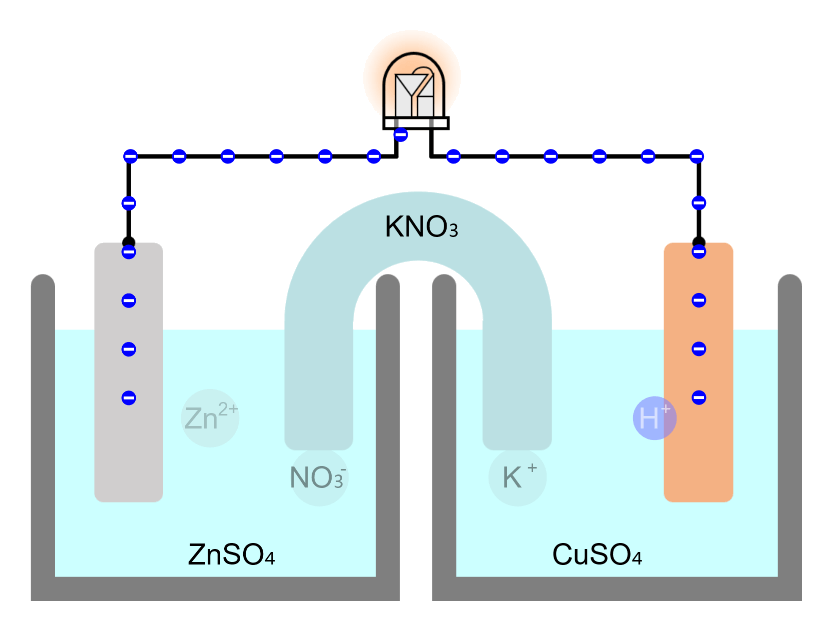
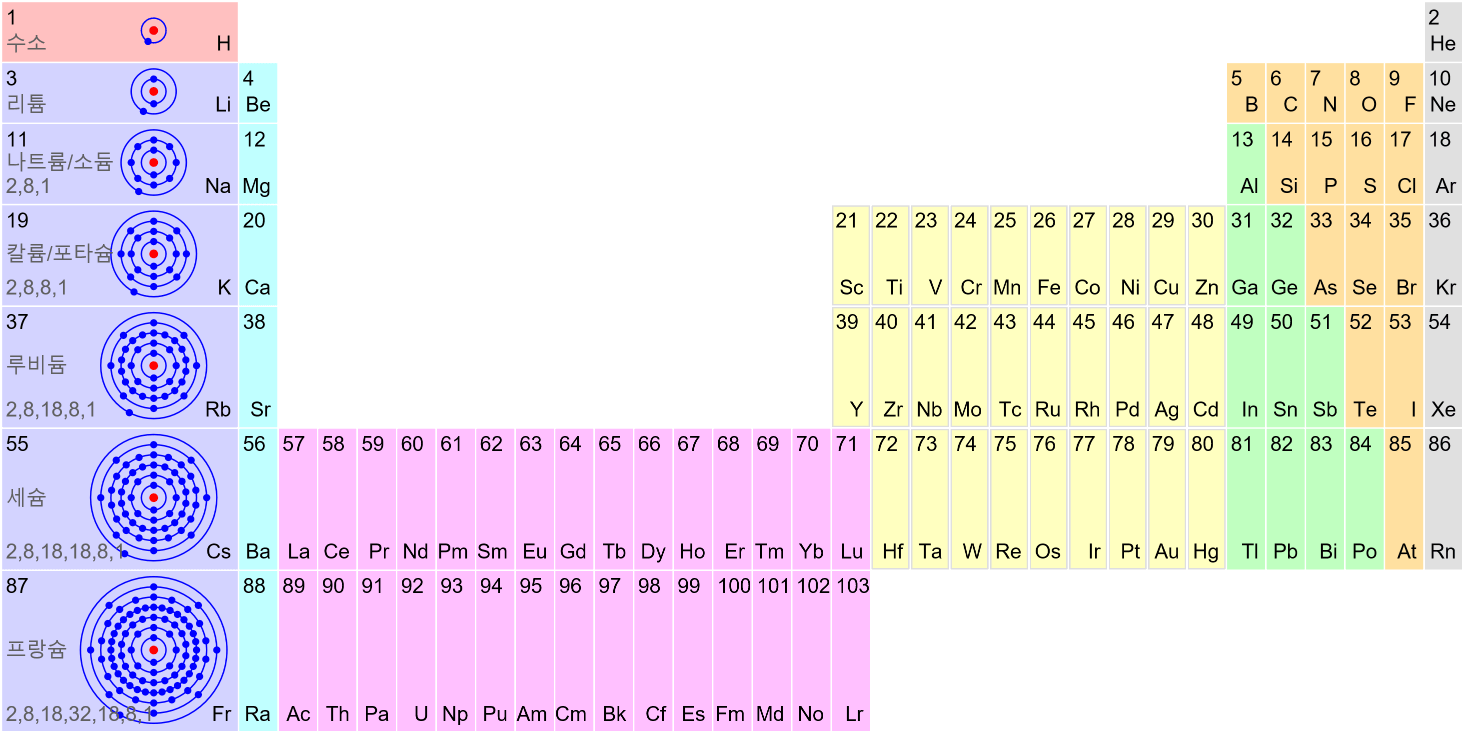Chemical Cell (Voltaic Cell, Daniel Cell)
Electricity production before Volta Before chemical cells, such as dry cells, there was only one thing we knew as a way to produce electricity. That is rubbing amber, glass, or metal. Voltaic Cell Alessandro Volta (1745-1827) … more