Root-Mean-Square Velocity of Gas Molecules (Vrms)

* The gas molecules in the above simulation are all of the same type, and the color of the molecules is for identification purposes only.

Kinetic Molecular Theory of Gases

‘Kinetic Theory of Gases’ is a hypothesis to explain the motion of gas molecules. To explain this hypothesis, we assume an ideal gas that satisfies the following assumptions:

1. Gas molecules have mass, but no volume.
2. Gas molecules do not exchange forces through space.
3. All collisions caused by gas molecules are perfectly elastic collisions.
4. Gas never liquefies or sublimes at any temperature or pressure.
5. The average kinetic energy of a gas molecule is proportional only to its absolute temperature and is not affected by the molecule’s size, shape, or type.

Root-Mean-Square Velocity of Gas Molecules

Assuming a box of length $L$ with a wall cross-sectional area $A$ contains a gas particle of mass $m$.

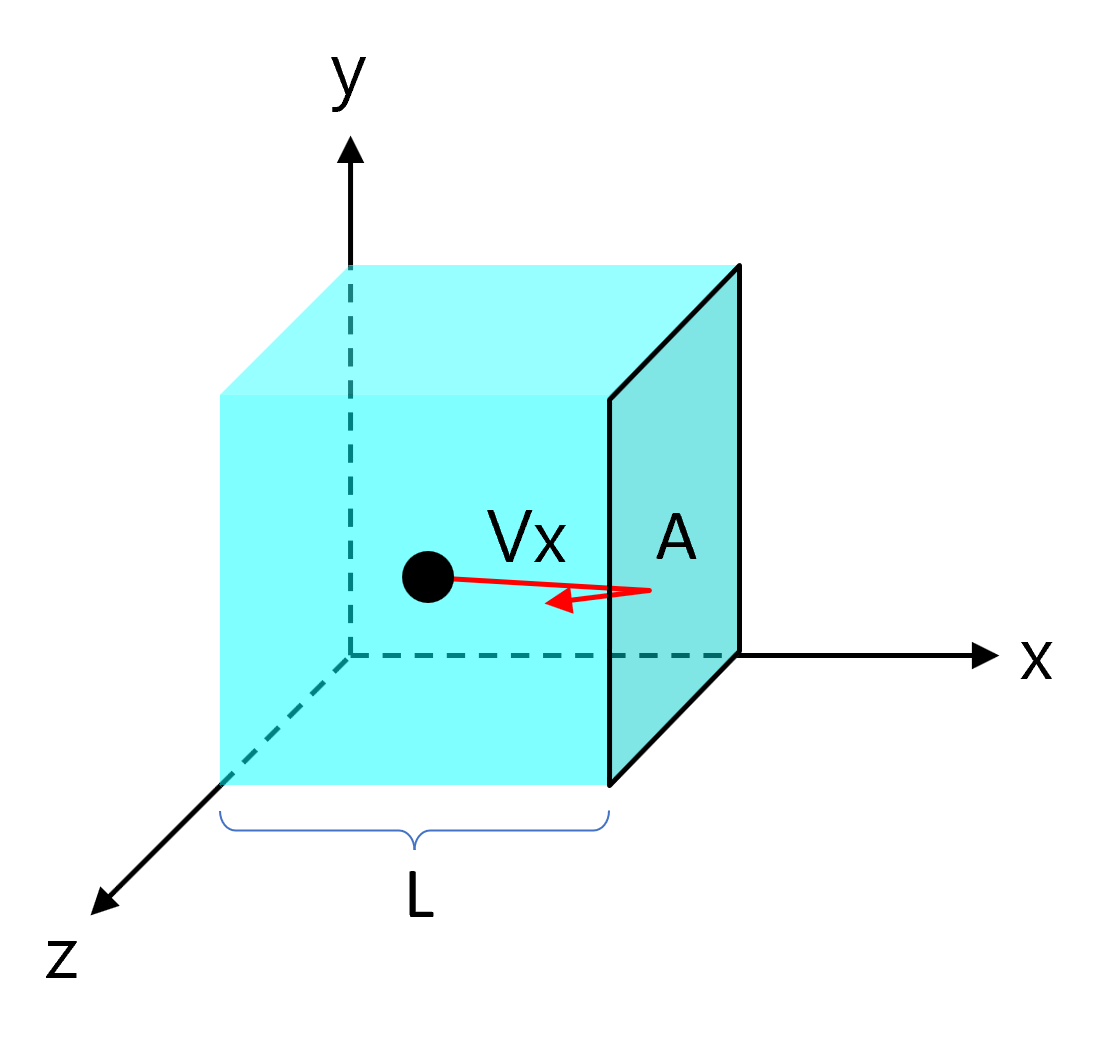
Gas particles collide with the wall entirely elastically and move linearly with random direction in the $x$, $y$, and $z$ axes.
Consider the case where a gas particle collides with the $A$ side with velocity $v_x$. The movement that applies an impact to the wall $A$ is only the $x$ axis component, so for the sake of convenience, the $y$ axis and $z$ axis are not considered for the time being.
A gas-particle makes a perfectly elastic collision with the wall $A$. The momentum of the particle before and after the collision changes as follows:

$$\Delta P_x = mv_x – (-mv_x) = 2mv_x$$

The time it takes for gas molecules to collide with one wall $A$, collide with the opposite wall, and collide with the wall $A$ again is as follows.

$$\Delta t = \frac{2L}{v_x}$$

The impact force $F$ on the wall $A$ per second can be obtained by dividing the momentum change by time.

$$F = \frac {\Delta p}{\Delta t} = \frac {2mv_x}{\frac{2L}{v_x}} = \frac{mv_{x}^{2}}{L}$$

Since the pressure $P$ on the wall $A$ is defined as the force per unit area, the pressure of the gas is as follows: (volume $V = AL$)

$$P = \frac{F}{A} = \frac{\frac{mv_x^2}{L}}{A} = \frac{mv_x^2}{AL} = \frac{mv_x^2}{V}$$

If there are two or more gas molecules, the magnitude of the pressure $P$ is as follows:

$$\begin{align} P &= \frac{mv_{x1}^2}{V} + \frac{mv_{x2}^2}{V} + \frac{mv_{x3}^2}{V} \cdots\\ &= \frac{m(v_{x1}^2 + v_{x2}^2 + v_{x3}^2 \cdots )}{V} \\ &= \frac{mN \overline{v_x^2}}{V} \end{align}$$

$N$ = number of gas molecules
$\overline{v_x^2}$ = The average value of the square of the velocity in the $x$ axis.

According to Pascal’s principle, the pressure of the gas is applied uniformly across all walls.
Thus, the pressure $P$ obtained above is equally applied to the entire wall of the box, not just for wall $A$.

Now, consider the direction of the $y$ and $z$ axes. The mean of the squared velocity of a gas particle ($v_{rms}^{2}$) can be expressed as the Pythagorean theorem.

$$\overline{v_{rms}^2} = \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2}$$

Since the motion of the ideal gases molecule has the same degrees of freedom in all axes, it can be thought of as follows.

$$\overline{v_{rms}^2} = 3\overline{v_x^2} \\ \therefore \overline{v_x^2} = \frac{1}{3}\overline{v_{rms}^2}$$

So, the pressure entire the box is as follows:

$$P = \frac{1}{3} \frac{mNv_{rms}^2}{V}$$

The total mass ‘$mN$’ can also be expressed as ‘$nM$'(=number of moles ($n$) × molar mass ($M$)).

$$P = \frac{1}{3} \frac{nMv_{rms}^2}{V} \\ \therefore PV = \frac{1}{3} nMv_{rms}^2$$

The above result should also agree with the ideal gas equation($PV=nRT$).

$$(PV=\,)\:\:\:\: \frac{1}{3} nMv_{rms}^2 = nRT$$

From the above equation, it can be seen that the ‘mean square velocity’ ($v_{rms}^2$) is proportional to the absolute temperature $T$ and inversely proportional to the molar mass ($M$).

$$\overline{v_{rms}^2} = \frac{3RT}{M}$$

‘Root-mean-square velocity'($v_{rms}$) is the square root of the mean square velocity ($v_{rms}^2$).

$$v_{rms} = \sqrt {\frac{3RT}{M}}$$

As such, ‘root-mean-square velocity’ can be clearly defined as a function according to the type of molecule and temperature.

Mean speed of gas molecules

The mean speed is the arithmetic mean of the speed of gas molecules. Momentum is conserved when two molecules collide, but their average speed continues to fluctuate. Assuming there are enough gas molecules, the average speed of the gas molecules is: (Derived from Maxwell-Boltzmann distribution equation)

$$< v > = \sqrt {\frac{8RT}{\pi M}}$$

The ‘mean speed’ has a slightly smaller value than the ‘root-mean-square velocity.’
And, the mean speed does not maintain a constant value and changes little by little. The smaller the number of molecules, the greater the fluctuation.