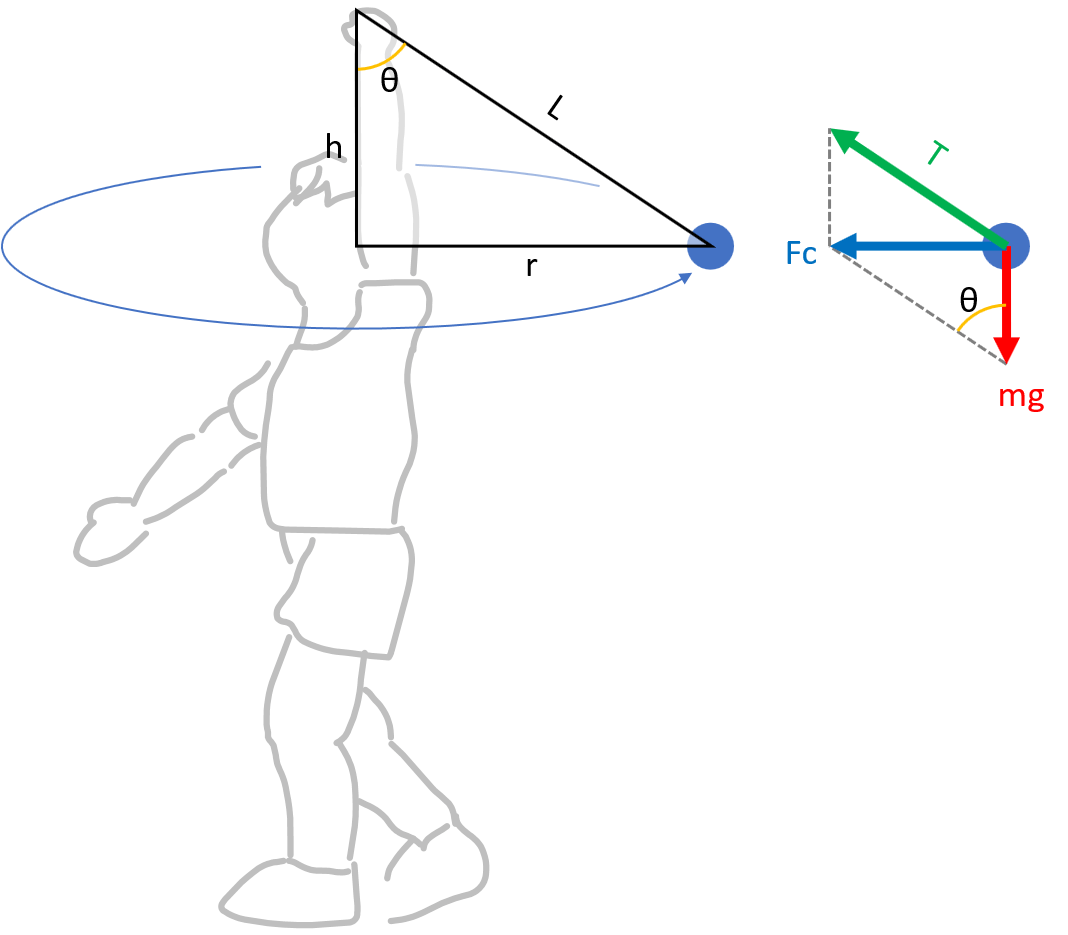
3 forces acting on a conical pendulum
- Gravity(=mg): The force the Earth pulls.
- Tension: The force applied to both ends of the thread. Tension is always directed to the center from both ends.
- Centripetal force(Fc): The force that maintains circular motion. The centripetal force always toward the center of rotation.
\[ F_{c} = mr \omega ^{2} = mr {( \frac{2\pi }{T})}^2 \]
ω: Angular velocity of rotational motion (rad/s)
T: period of rotational motion (seconds)
Find the period of a conical pendulum
Consider a conical pendulum with a line length ‘L’ and a rotation radius ‘r.’
Centripetal force(Fc) is the result of gravity and tension. Also, the centripetal force is perpendicular to gravity. From this, the following equation is calculated.
\[ F_{c} = mg \cdot tan \theta \]
Substituting the definition of centripetal force comes the following equation.
\[ mr {( \frac{ 2 \pi }{T})}^2 = mg \cdot tan \theta \]
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g }{r} \cdot tan \theta \]
Since it is \( tan \theta = \frac{r}{h} \), we can make it a bit simpler.
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g}{h} \]
Solving the above equation for the period T, It becomes as follows.
\[ T = 2 \pi \sqrt{\frac {h}{g}} \]