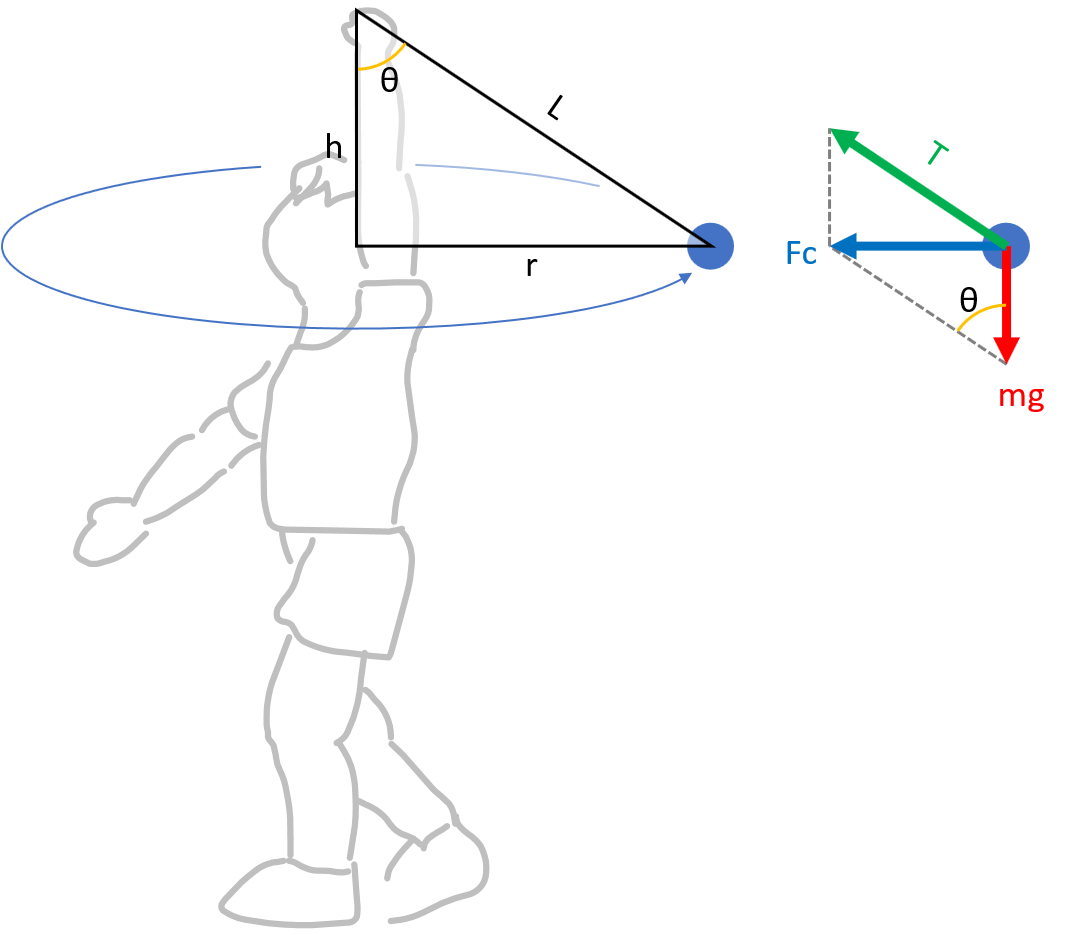
円錐振り子に作用する3つの力
- 重力(=mg):地球が引っ張る力です。
- 張力:糸の両端にかかる力です。張力は、糸の両端から中心方向に向かいます。
- 求心力(Fc):円運動を維持させる力です。求心力は常に回転の中心方向を向きます。
\[ F_{c} = mr \omega ^{2} = mr {( \frac{2\pi }{T})}^2 \]
ω:回転運動の角速度(rad/ s)
T:回転運動の周期(秒)
円錐振り子の周期
行の長さが「L」、回転半径が「r」である円錐振り子を考えてみます。
求心力「Fc」は、重力と張力の合力です。また、求心力は、重力と垂直です。したがって、次のような式が算出されます。
\[ F_{c} = mg \cdot tan \theta \]
求心力の定義を代入すると、以下の式が作成されます。
\[ mr {( \frac{ 2 \pi }{T})}^2 = mg \cdot tan \theta \]
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g }{r} \cdot tan \theta \]
\( tan \theta = \frac{r}{h} \) ので、もっと簡単にすることができます。
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g}{h} \]
上記の方程式を回転運動の周期「T」に対して解いてみれば、次のようになります。
\[ T = 2 \pi \sqrt{\frac {h}{g}} \]