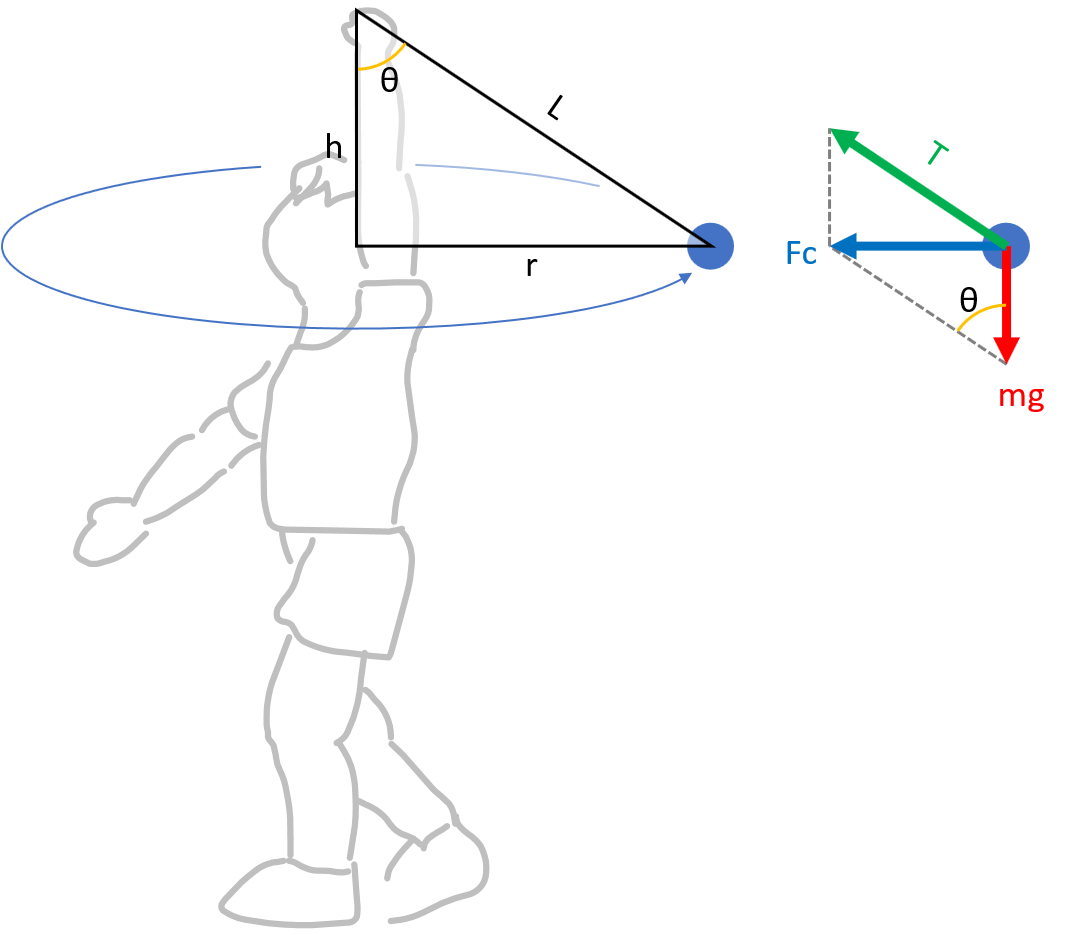
원뿔 진자에 작용하는 3가지 힘
- 중력(=mg): 지구가 당기는 힘입니다.
- 장력: 실의 양 끝에 걸리는 힘입니다. 장력은 항상 실의 양 끝에서 가운데 방향으로 향합니다.
- 구심력(Fc): 원운동을 유지시키는 힘입니다. 구심력은 항상 회전의 중심 방향을 향합니다.
\[ F_{c} = mr \omega ^{2} = mr {( \frac{2\pi }{T})}^2 \]
ω: 회전 운동의 각속도 (rad/s)
T: 회전 운동의 주기 (초)
원뿔 진자의 주기 구하기
줄의 길이가 ‘L’이고, 회전 반지름이 ‘r’인 원뿔 진자를 생각해 봅니다.
구심력 ‘Fc’는 중력과 장력의 합력입니다. 또한 구심력은 중력과 수직입니다. 이로부터 다음과 같은 식이 산출됩니다.
\[ F_{c} = mg \cdot tan \theta \]
구심력의 정의를 대입하면 아래의 식이 만들어집니다.
\[ mr {( \frac{ 2 \pi }{T})}^2 = mg \cdot tan \theta \]
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g }{r} \cdot tan \theta \]
\( tan \theta = \frac{r}{h} \) 이므로, 좀 더 간단하게 할 수 있습니다.
\[ {( \frac{ 2 \pi }{T})}^2 = \frac {g}{h} \]
위 방정식을 회전 운동의 주기 T에 대해서 풀어보면 아래와 같이 됩니다.
\[ T = 2 \pi \sqrt{\frac {h}{g}} \]