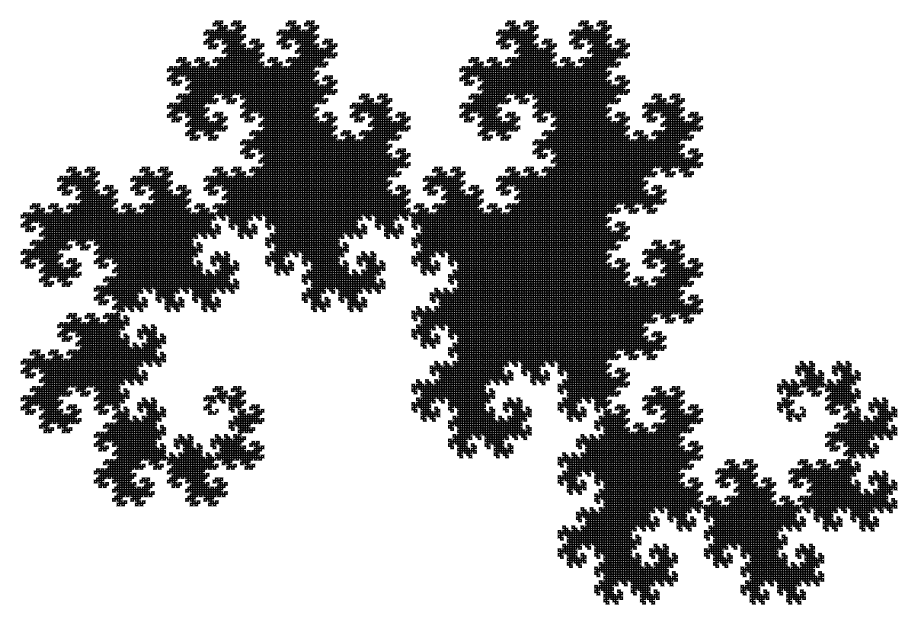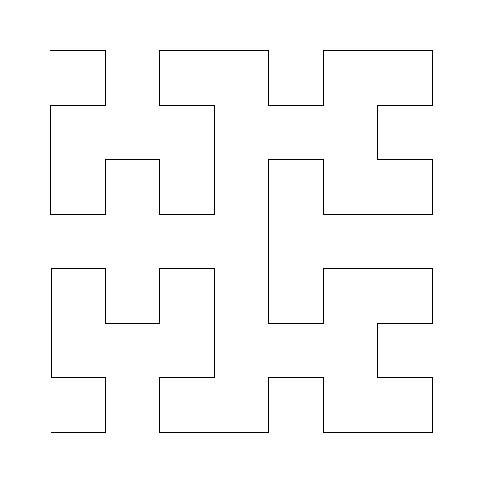프랙털 시뮬레이션
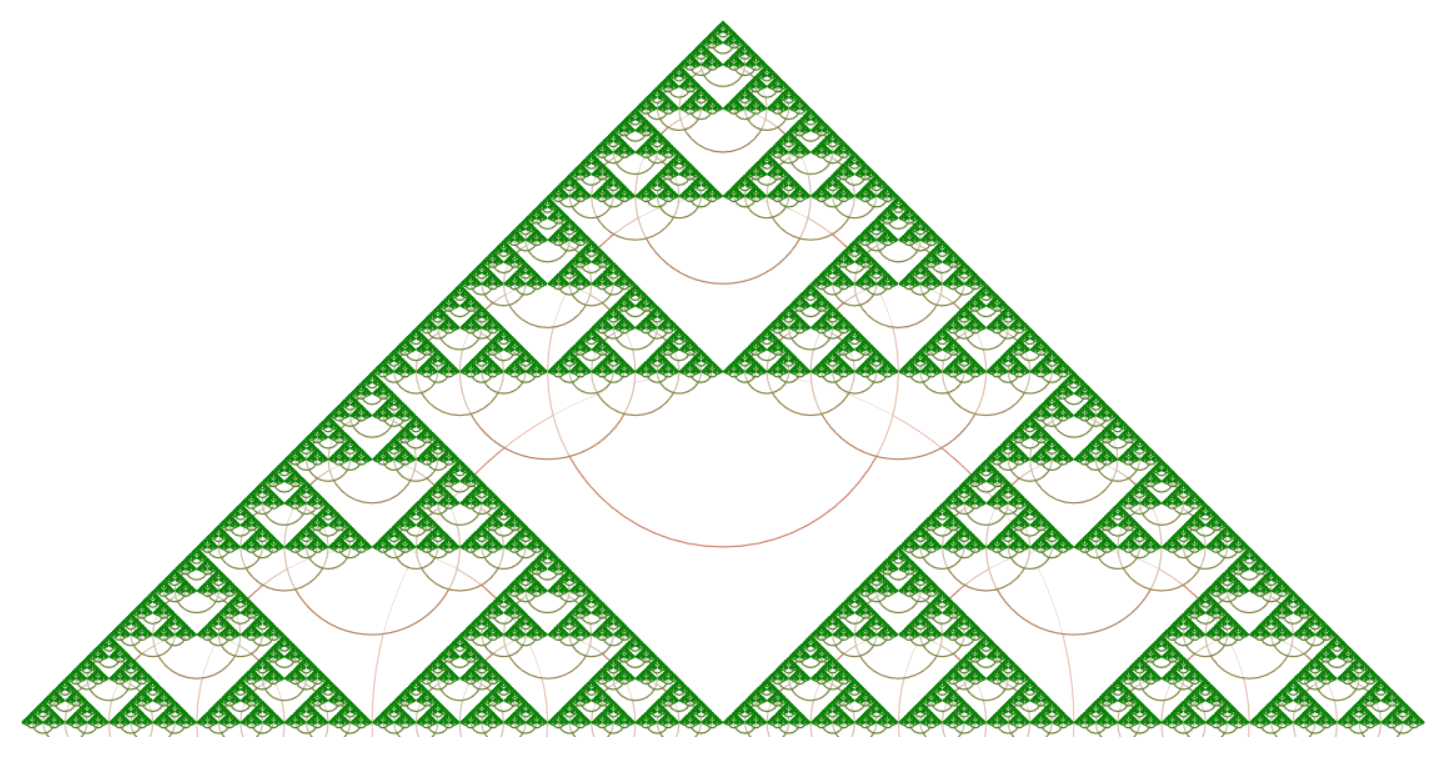
시어핀스키 삼각형
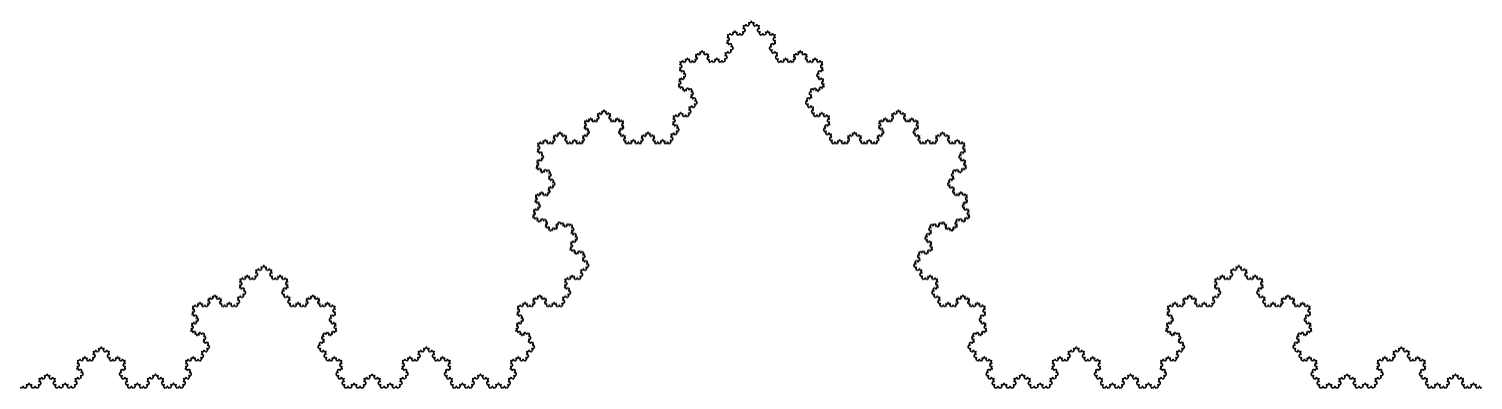
시어핀스키 곡선 폴란드의 수학자 바츠와프 시어핀스키(또는 시에르핀스키, 1882-1969)의 이름이 붙은 프랙털 도형입니다. 모양을 자세히 보면 부분과 전체가 서로 닮아 있습니다. 부분들의 모습이 되풀이 되어 전체모습이 된다는 것은 프랙탈의 기본 원리에 해당됩니다.
드래곤 커브
드래곤 커브 드래곤 커브란 종이 테이프를 그림과 같은 방향으로 몇 번 접은 다음, 꺽이는 곳이 직각이 되도록 한 곡선을 말합니다. 이 곡선은 자신과 접하는 일은 있어도, 교차하지는 않습니다. 접는 회수가 커지면 복잡한 도형이 됩니다.
Hilbert 커브
힐베르트 곡선은 1891 년 독일 수학자 데이비드 힐베르트가 처음으로 설명한 프랙탈 곡선입니다. 프랙탈의 자기유사성 프랙탈 곡선들은 크게 확대하더라도 원래의 모습을 그대로 유지하고 있습니다. 대부분의 프랙탈 곡선들은 동일한 변형을 점점 더 작은 규모로 반복하여 만들어 냅니다. 규모가 달라지더라도 원래의 모습을 유지한다는 … more