The principle of riding a swing

Kids have the know-how, but they can’t tell the principal.

“How can you go so high?”
Some principles are difficult to describe in words in the world, even if everyone knows.
I think one of them is how to ride a swing.
Can you explain how to ride a swing with a physics equation?

Standing or sitting at the midpoint of a moving swing changes the length of the pendulum.
In other words, a swing can be thought of as a ‘pendulum that can change its length‘.
Consider the pendulum that moves, as shown in the picture below.

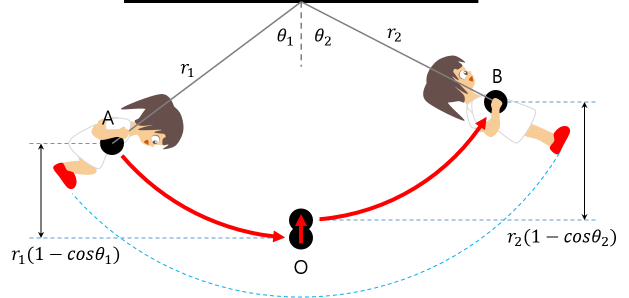
When you going down from A to O

The reduced potential energy equals the increased kinetic energy.
$$mg r_1 (1 – cos \theta_1 ) = \frac{1}{2}mv^2 \\ v^2 = 2gr_1 (1 – cos \theta_1 )$$

When you going from O to B.

Reduced kinetic energy equals increased potential energy.
$$\frac{1}{2}mv^2 = mg r_2 (1 – cos \theta_2 ) \\ v^2 = 2gr_2 (1 – cos \theta_2 )$$

Change in angle while moving from A to B

The speed at ‘O’ does not changed,
$$2g r_1 (1 – cos \theta_1 ) = 2g r_2 (1 – cos \theta_2 ) \\ r_1 (1 – cos \theta_1 ) = r_2 (1 – cos \theta_2 )$$ $$\therefore \theta_2 = cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}})$$

How to ride a swing well?

When going down, we need to increase the length of $r$. (= sit down.)
Conversely, when you go up, you have to stand up.
For example, let’s calculate the increase in angle by substituting the following condition.

• $r_1 = 3m$
• $r_2 = 2m$
• $\theta_1 = 45˚$ (Angle of starting point)

$$\begin{align} \theta_2 &= cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}}) \\ &= cos^{-1} ({\frac{2 – 3(1 – cos 45˚)}{2}}) \\ &\approx 55.9˚ \end{align}$$

In this case, the angle is increased by about 1.24 times.