子供も知っているブランコの裏技
「どのようにすればそんなに高く上がることができる?」
世の中には、誰もが知っているが、その原理を説明するのが難しいことがあります。
ブランコに乗る方法もその一つです。
ブランコに乗る方法を物理的に説明できますか?
動くブランコの中間地点で立ち上がるだり、座っだりすれば、振り子の長さが変わります。
つまり、ブランコは、長さを変化させることができる振り子と考えることができます。
下の図のように運動する振り子の長さが途中で変わる場合を考えてみましょう。
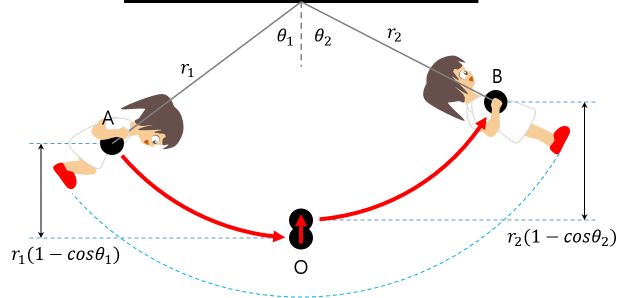
A → Oで下がる場合
減少された位置エネルギーは増加された運動エネルギーと同じです。
\[ mg r_1 (1 – cos \theta_1 ) = \frac{1}{2}mv^2 \\ v^2 = 2gr_1 (1 – cos \theta_1 ) \]
O → Bに上がる場合
減少された運動エネルギーは増加された位置エネルギーと同じです。
\[ \frac{1}{2}mv^2 = mg r_2 (1 – cos \theta_2 ) \\ v^2 = 2gr_2 (1 – cos \theta_2 ) \]
A → Bに移動する間の角度の変化
O点での速度は変わらないので、
\[ 2g r_1 (1 – cos \theta_1 ) = 2g r_2 (1 – cos \theta_2 ) \\ r_1 (1 – cos \theta_1 ) = r_2 (1 – cos \theta_2 ) \] \[ \therefore \theta_2 = cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}}) \]になります。
ブランコをよく乗るための方法は?
下がるとき、「r」の長さを増加させます。(つまり、座ります。)
逆に、上がる時は、立ち上がります。
たとえば、次のような条件で角度の増加量を計算してみると、
- \( r_1 = 3m \)
- \( r_2 = 2m \)
- \( \theta_1 = 45˚ \) (出発地点の角度)
\[ \begin{align} \theta_2 &= cos^{-1} ({\frac{r_2 – r_1(1 – cos \theta_1)}{r_2}}) \\ &= cos^{-1} ({\frac{2 – 3(1 – cos 45˚)}{2}}) \\ &\approx 55.9˚ \end{align} \]
この場合には、角度が約1.24倍に増加します。