- This simulation supports both pinch zoom and mouse scrolling.
- We recommend using the Chrome browser. (to get more processing speed)
Imaginary number
An imaginary number consists of a number that becomes negative if you square itself.
The letter ‘ i’ represents an imaginary number. This means that the imaginary number doesn’t exist.
\[ i^{2} = -1 \]
Imaginary numbers are a whole new number system different from actual numbers. This is because they become positive numbers when you square real numbers.
Imaginary numbers are not numbers that exist in the real world. But, it comes logical error-free and can calculate using a computer.
You can indicate the imaginary scale by prefixing the imaginary numbers with real numbers. (ex. i, 2i, 3i, 1.5i). But you can’t compare the magnitude of an imaginary number. That is, ‘2i’ is not bigger than i. This is because imaginary numbers are neither positive nor negative.
\[ (bi)^{2} = b^{2}\,i^{2} = -b^{2} \]
Complex number
A complex number is a number like ‘a + bi’ that mixes a real number and an imaginary number.
If ‘b = 0’ in the complex ‘a + bi,’ only the real part remains.
If ‘a = 0’ in the complex ‘a + bi,’ the real part disappears, and only the pure imaginary ‘bi’ remains.
Representation of a complex number
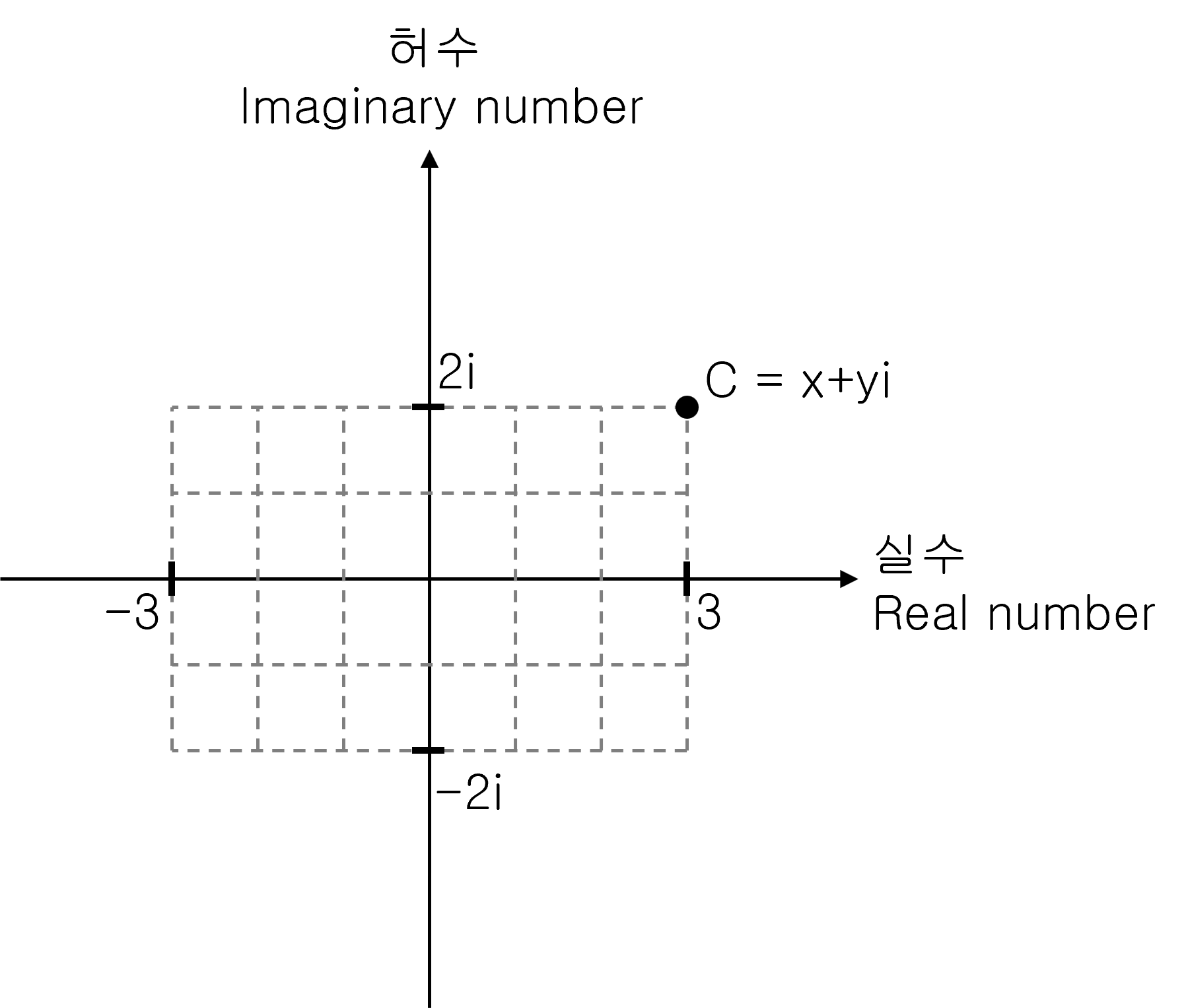
We can point to a complex number in the plane. In other words, the x-axis is the axis that represents the real number, and the y-axis that is perpendicular to the x-axis represents the imaginary number.
Pure real numbers then correspond to the horizontal axis. And pure imaginary numbers correspond to the vertical axis. And complex number corresponds to one point on the plane, not the axis.

Mandelbrot Set
Let’s learn about the Mandelbrot equation. Mandelbrot’s equation is a straightforward equation with only two variables, ‘Z’ and ‘C.’
\[ Z_{n+1} = {Z_n}^{2} + C \]
Square the complex number ‘Z’ and add ‘C’ to it to create a new ‘Z.’ Square the newly created ‘Z’ and then add ‘C’ to it again to make a new ‘Z.’ Repeat this infinitely.
Mandelbrot found that the value of ‘Z’ continued to increase or to shuttle between two small imaginary numbers (depending on the value of ‘C’). He used a computer to represent each ‘C’ value on the screen as a point on which ‘Z’ does not radiate. The result is something far from purely geometric shapes (squares, triangles, circles). This is called Mandelbrot’s set.
Mandelbrot continued to magnify the image, but the same structure continued to appear. Even after zooming in forever, the same shape and form continued to emerge.

How to draw Mandelbrot’s set
First, set a complex coordinate (x, y) on one pixel of the computer screen and call it ‘C (= x, yi).’ Usually, the ‘x’ value ranges from -3 to +3, and the ‘y’ value ranges from -2 to +2.
With this range, you can see the whole view of Mandelbrot’s set.
If the values that Z does not diverge represent as black dots on the screen, the result is a Mandelbrot set. Usually, if it is larger than 2 ~ 4, it is regarded as diverging and stops the recurrence relation.
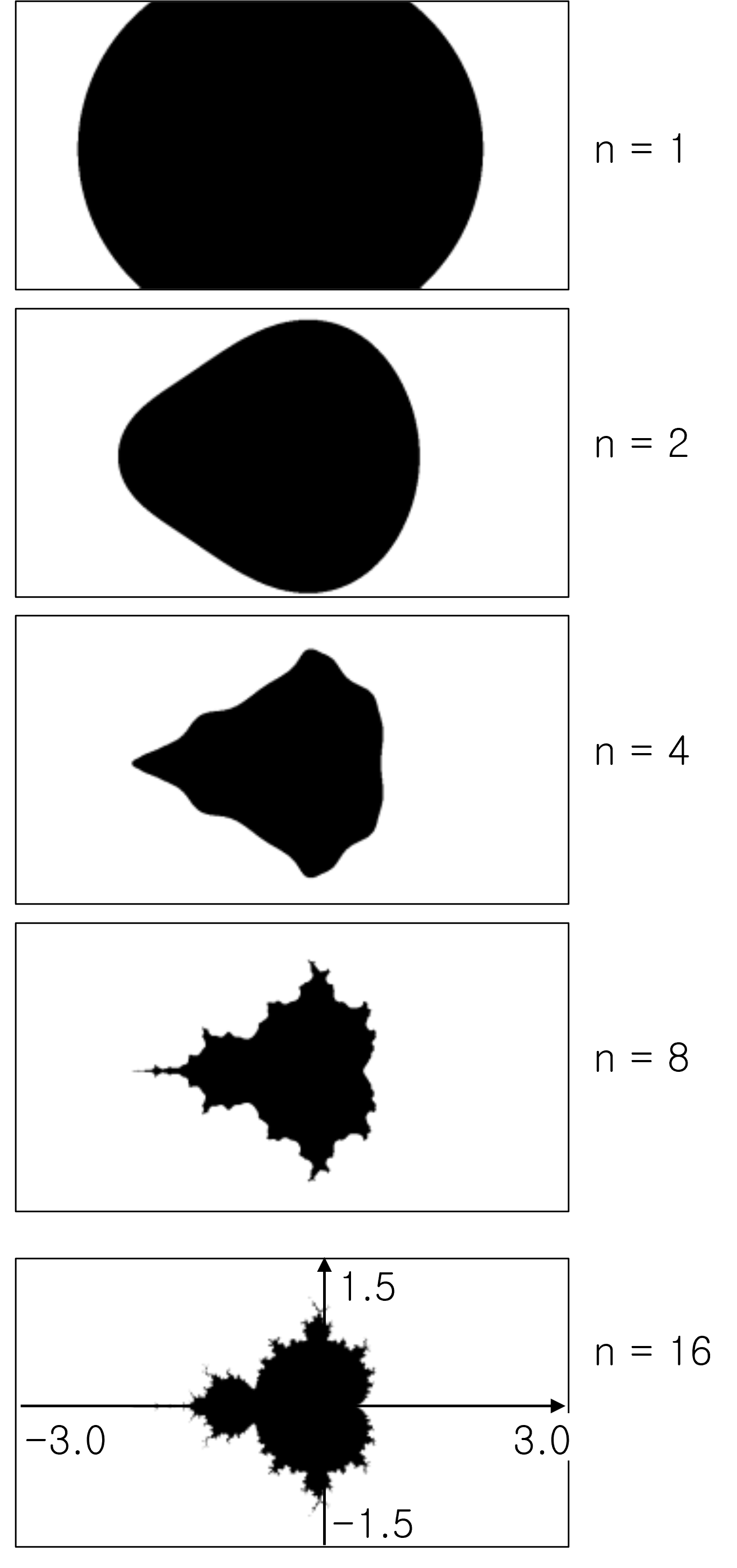
The more you repeat the recurrence relation, we can get a more fine picture.
However, it cannot be calculated indefinitely due to computing power limitations, so it stops at a reasonable level.
You can get an artistic picture if an appropriate color is applied to the screen according to the Iteration number when the divergence is determined. Currently, Mandelbrot’s set becomes the main material for graphics that utilize the computer’s computing power along with Julia’s set.
