Fourier series
The Fourier series is an infinite series that expresses a periodic function that repeats a certain part as the sum of simple trigonometric functions.
A simple trigonometric function consists of a smooth surface wave. If you keep adding these trigonometric functions, you can get a function of a different shape.
For example, let’s create a square wave using a Fourier series.
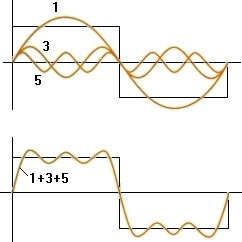
As shown in the picture above, you can get a shape close to the square wave by adding 3 normal trigonometric functions. Listed in the form, it is as follows.
\[ f(x)\, =\, sin(x)\, +\, \frac {1 }{ 3} sin(3x)\, +\, \frac {1 }{ 5} sin(5x) \]
Right now, it’s just three functions added, so it’s a bit insufficient to say that it’s a full square shape.
However, if you can add infinitely in this way, you will eventually get a clean function form.
\[ \begin{align}
f(x)\, &=\, sin(x)\, +\, \frac {1 }{ 3} sin(3x)\, +\, \frac {1 }{ 5} sin(5x)\, +\,… \\
&=\, \sum _{ n=0 }^{ \infty }{ \frac {1 }{ (2n+1)} sin((2n+1)x)}
\end{align} \]
Application of Fourier series
The Fourier series is mainly used to obtain a specific waveform in an electronic circuit.
For example, the Fourier series for square waves and sawtooth waves are:
