- Switch up to start charging, and switch down to start discharging.
- The measured voltage is recorded automatically when charging or discharging starts.
- You can change the measuring point by moving the probe.
- For accurate measurement, operate the switch after fully charging or discharging the capacitor.
- To prevent fluctuations in the measured value, do not change the voltage, resistance, or capacitance during measurement.
Charging the capacitor
While you apply voltage to a capacitor, current flows through it.
The process of charging accumulates electric charges, and the internal voltage rises by this accrued charge.
As charging progresses, the charging rate slows down, and the internal voltage approaches the external voltage.
While charging, the voltage changes as follows:
\[ V(t)=V_0 (1-e^{-t/RC}) \]
\(V(t)\) : Capacitor internal voltage (V)
\(V_0\) : External voltage (V)
\(t\) : Time (seconds)
\(R\) : Resistance (Ω)
\(C\) : Capacitance (F)
For example, if the external voltage is 1 V, the resistance is 1 kΩ, and the capacitance is 1000 μF, the following characteristic curve can be obtained.
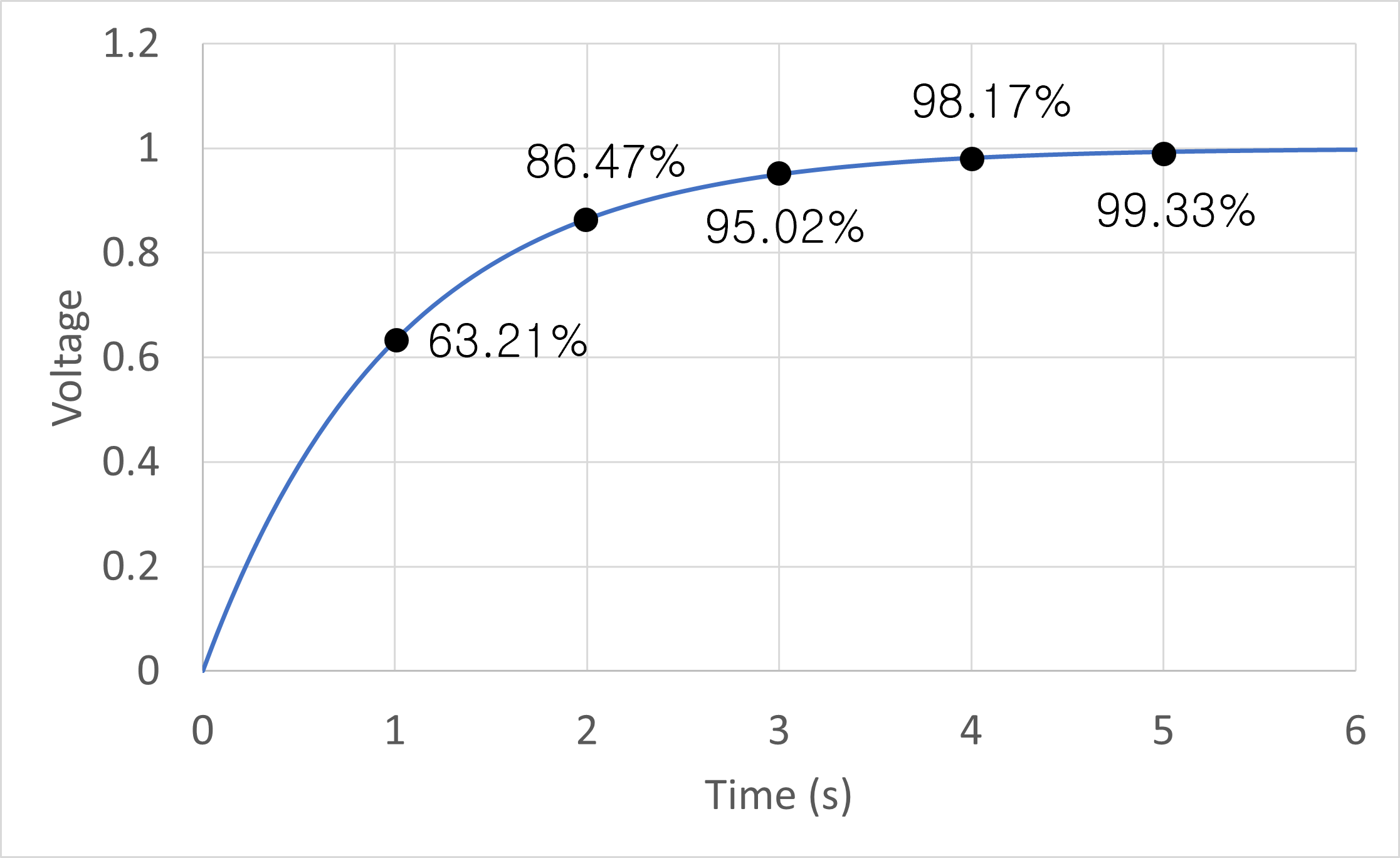
\(RC\) multiplied by resistance and capacitance is called the time constant (τ). The time constant has the following characteristics.
- When charging during the 'time constant,' approximately 63.21% of the capacity is charged.
- If you charge about 5 times the 'time constant,' about 99.33% will be charged.
- The larger the resistance, the weaker the current flows. So it takes longer to charge.
- The larger the capacitance, the greater the need to charge it. So It takes a long time.
Discharging the capacitor
Discharge of the capacitor also takes time.
Discharging a capacitor can be thought of as similar to charging.
That is, about 63.21% of the total capacity is discharged during the time constant, and when it is discharged about 5 times the time constant, approximately 99.33% of the capacity is discharged.