Minkowski Spacetime
Minkowski spacetime (or Minkowski space) is a coordinate system devised by German mathematician Minkowski. The peculiar thing is that the coordinate system contains space and time.
Minkowski spacetime uses matrices to express a four-dimensional coordinate system (x, y, z, ct) by integrating three-dimensional space and time. However, because 4D matrices are very complex, they usually only deal with motion in one axis (e.g., the x-axis). Then, the horizontal axis became the x-axis of space, and the vertical axis became the y-axis of time(x, ct).
Minkowski spacetime makes it easy to explain time dilation phenomena according to 'Special Relativity,' such as the 'twin paradox.'
Please refer to the link below for a post on the twin paradox.
Understanding Minkowski space
When introducing a Minkowski space, it is important to keep the following in mind:
- Observers observe objects around them based on their own coordinate system.
- The speed of light is the same in any coordinate system.
- For the speed of light to be the same, the axes of the coordinate system can be curved or tilted.
For example, let's say a very fast (half the speed of light) spaceship departs from Earth and is moving at a constant velocity.
In terms of Earth?

The blue bands are time zones relative to Earth.
The Earth is stationary, and the spaceship keeps moving away from it.
Because the time in a moving spaceship is slower than Earth, It gradually moves away from Earth's time zone.
The Earth and spaceship's motion can be represented by points on the Minkowski plane.
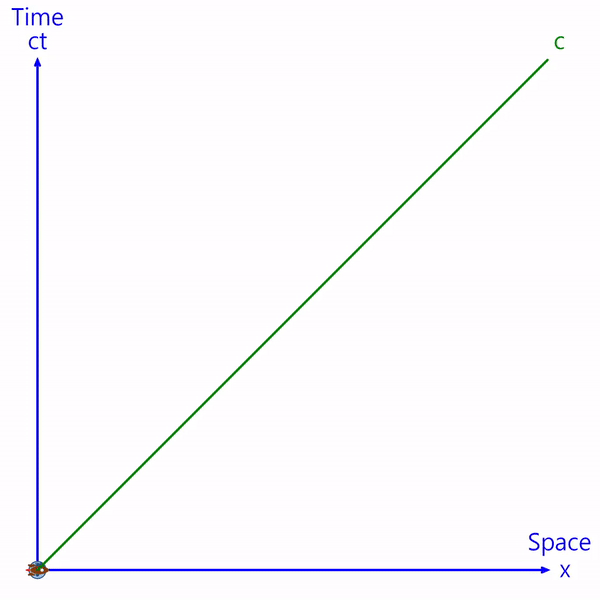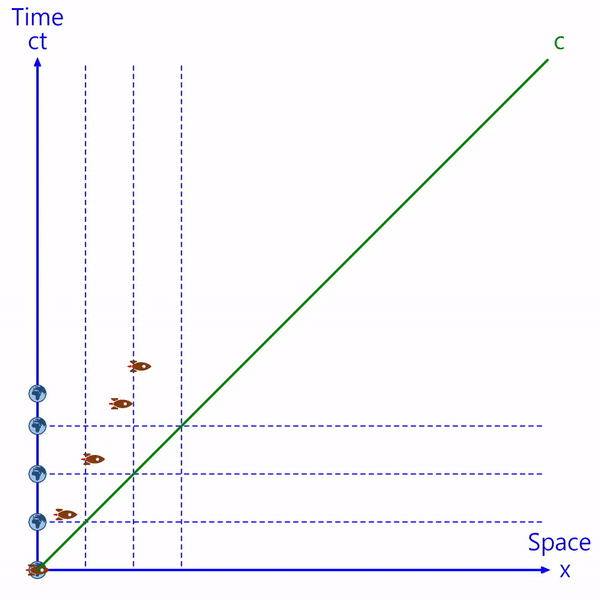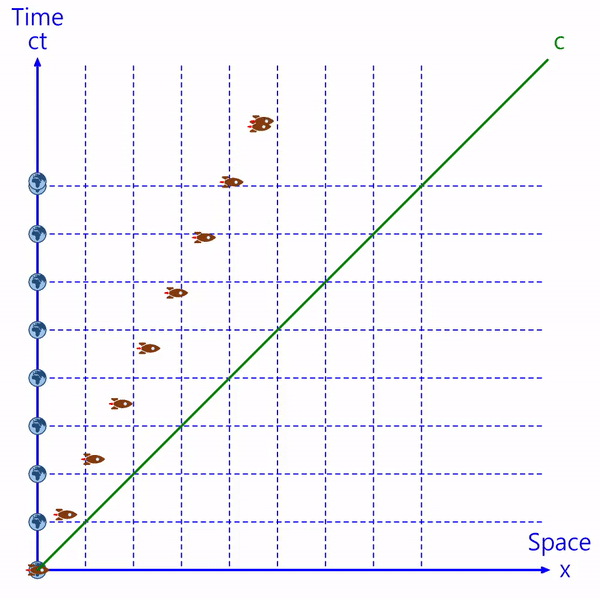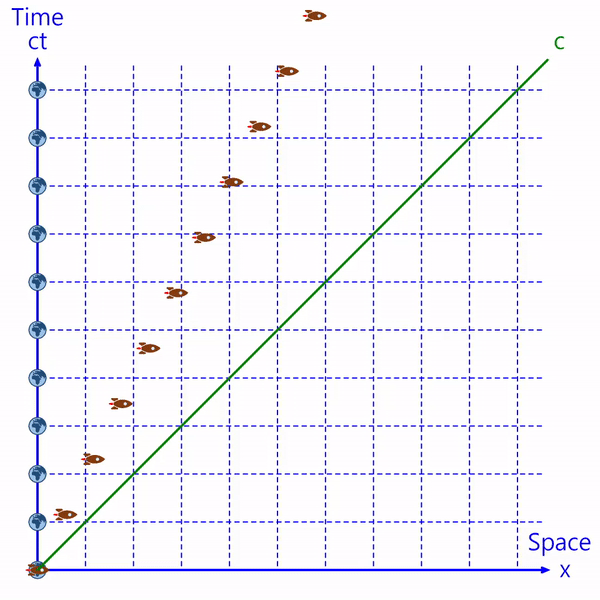
The horizontal axis represents the space where the object is located, and the vertical axis represents the time of the object. (The vertical axis is expressed as 'ct' by multiplying time by the speed of light. It is also described as 'ict' including imaginary numbers.)
Since the Earth is stationary, the Earth is located on the time axis.
Since the speed of any object cannot be faster than light, the spaceship's position in spacetime is to the left of the speed of light (c).
In terms of spaceship?
The relative position of the spacecraft is '0'. Therefore, the spacecraft is located on the time axis (ct').
From the spaceship's point of view, what is the speed of light?
According to Special Relativity, the speed of light does not change when the coordinate system changes. In other words, the slope (c) is constant.
The time axis (ct') is already tilted. For the speed of light to remain constant, the spatial axis (x') must also be tilted.

Therefore, the spacetime coordinate system based on the spaceship is transformed as follows (red).

If the two coordinate systems are superimposed, it is as follows.
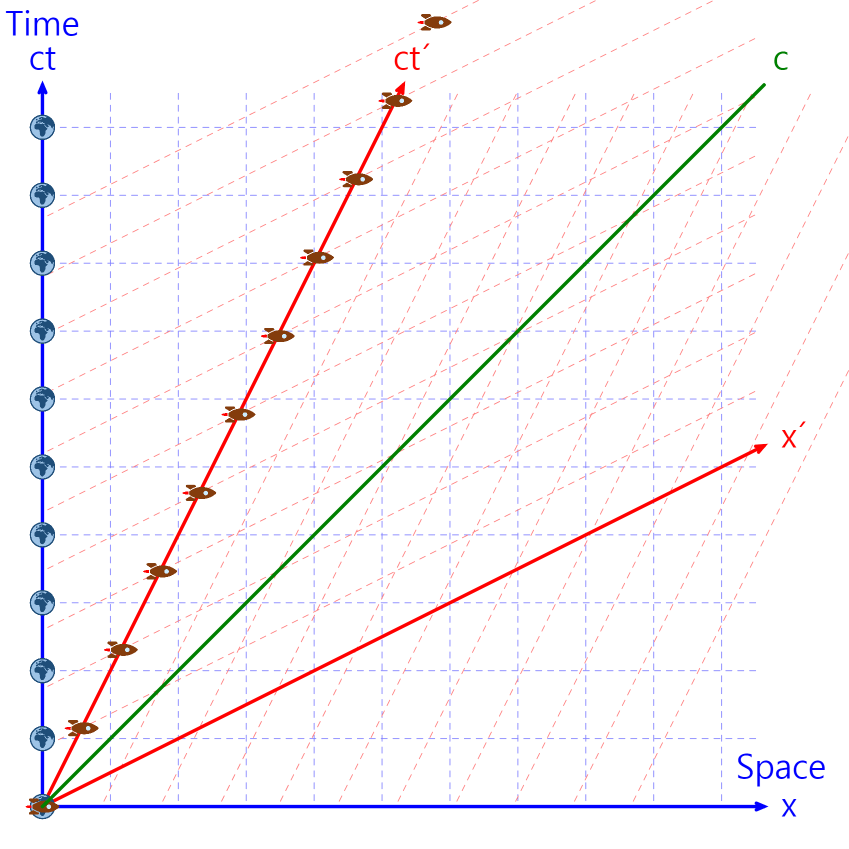
The blue line is the coordinate system relative to the Earth, and the red is the coordinate system relative to the spaceship.
The graph above explains the following phenomena.
- The Earth and the spaceship are positioned on the time axis in their respective coordinate systems.
- The speed of light is constant regardless of the coordinate system.
- The Earth and spaceship are viewed each other's time passing slowly.
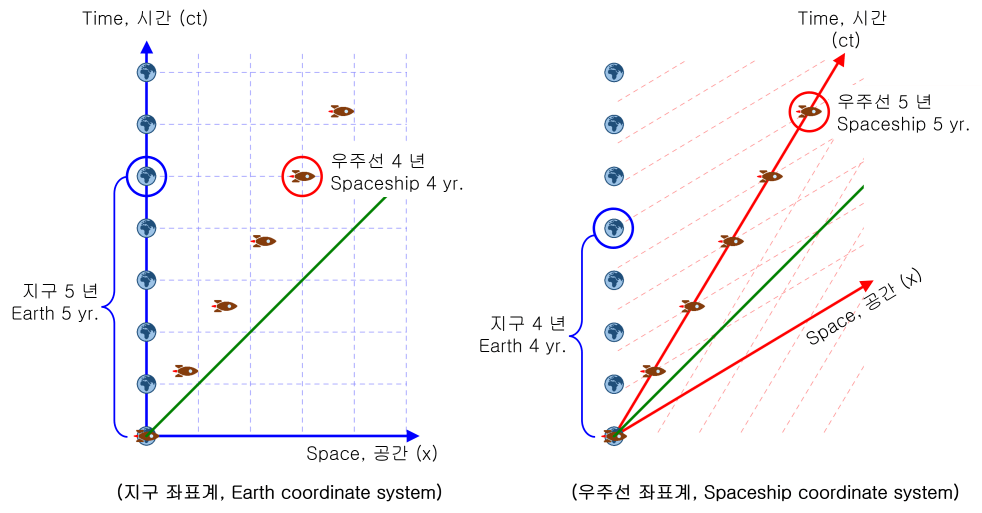
The figure above shows a spacecraft moving away from Earth at 0.6 times the speed of light. The two figures are the same motion; only the coordinate system is observed differently.
From the earthman's point of view, the spacecraft's time passes slowly.
However, from the astronaut's point of view, Earth's time flows slowly.
This is because each observes the other through their coordinate system.