The meanings of the symbols used in this simulation are as follows.
- L = Distance that light travels in a stationary state, (=ct。)
- c = Speed of light (≒ 299,792,458 m/s)
- t。 = The transit time of light observed inside the spacecraft(or the transit time of light observed in a stationary state)
- t = The transit time of light observed inside the spacecraft
- v = The speed of the spaceship
Special relativity
'Special relativity' is a physics theory that deals with objects moving very fast, such as the speed of light. As velocity increases, some phenomena that classical mechanics cannot explain (Newtonian mechanics) appear. The theory to explain this is 'Special relativity,' perfectly compatible with classical mechanics.
Special relativity started with the idea of Albert Einstein, a famous physicist that everyone knows.
Conditions
Special relativity starts with two conditions:
- In any inertial system, the laws of physics apply equally.
An 'inertial system' refers to a space with no change in speed, such as a train running at a constant speed.
The laws of physics that apply outside the train (law of inertia, F=ma, action-reaction, (angular) momentum, conservation of energy, etc.) also apply equally inside the train. In fact, even assuming the train is stationary and moving is the scenery outside the train, there is no way to figure it out. - The speed of light is the same no matter which inertial system you observe.
Imagine that some light is emitted from a very fast-moving spaceship. If the speed of light observed from the spacecraft is \(c\) and the speed of the spaceship is \(u\), the speed of light observed from the outside is likely to be \(u+c\), but the speed of light is It will still be \(c\). Even if this light is observed in another inertial system, it is still \(c\).
What happens with Special relativity
According to Special relativity, some interesting things happen:
- Time dilation: In an inertial system moving at high speed, time is observed to pass slowly.
- Length contraction: In an inertial system moving at high speed, it is observed that the length of the moving direction axis is shortened.
Time dilation
Time inside an object moving at high speed flows slowly.
Of course, all inertial systems are equal, so if you look at outer space from a spacecraft, you observe that time in external space moves slowly.
Consider a spaceship that is moving at a very high speed.
When the spacecraft is stationary
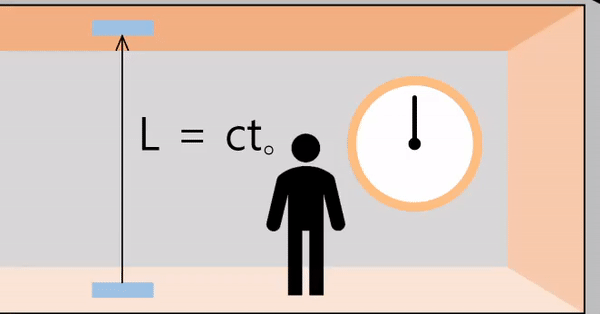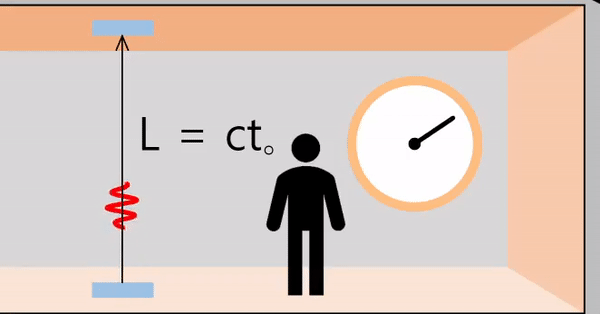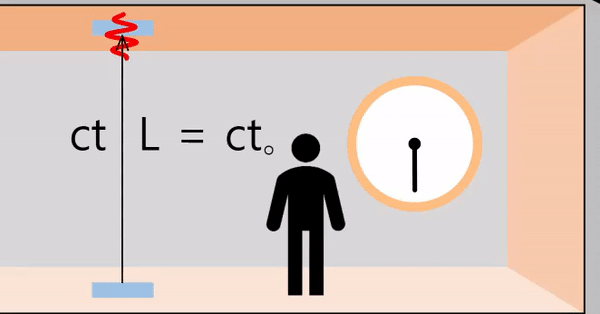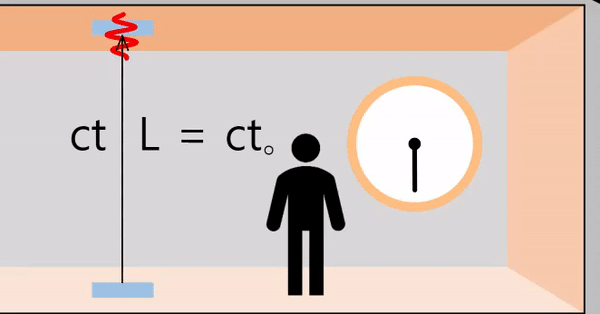
The inside and outside of the spacecraft are the same inertial system.
Assuming that the light emitted from the bottom of the spacecraft travels to the ceiling, the distance the light travels is ('distance = speed × time')
\[L = ct_o\]
If the spacecraft is moving with speed \(v\)

The distance the light travels is the same as if the spacecraft were stationary (vertical direction independent of the direction of movement of the spaceship).
\(t_o\) = The transit time of light observed inside the spacecraft.
\[L = ct_o\]
From the outside, the spacecraft is moving at the speed \(v\). Therefore, light travels on a hypotenuse path, and the travel distance can be obtained as follows.
\(t\) = The transit time of light observed outside the spacecraft.
\[hypotenuse = ct\]
Since the moving distance of the spacecraft seen from the outside is \(vt\), we can make the following equation using the Pythagorean principle.
\[{(ct)}^2 = {(ct_o)}^2 + {(vt)}^2\]
Solving the above expression for \(t\) gives the following expression:
\[t = \frac{t_o}{\sqrt{1-\frac{v^2}{c^2}}}\]
\(t\) of a moving object is always longer than \(t_o\). That is, the time in a moving inertial system is dilated.
In everyday life, speed is much slower than light. So, the effect of time delay in daily life is almost '0'.
Length contraction
For an explanation of length contractions, please refer to the link below.