CAUTION: Read the following instructions to the end to get the result that the moving object appears to be constricted in length. (It is difficult to explain 'Special Relativity' only with the above simulation.)
The meanings of the symbols used in this simulation are as follows.
- L。 = Distance that light travels in a stationary state (=ct。)
- c = Speed of light (≒ 299,792,458 m/s)
- t。 = The transit time of light observed inside the vehicle(or the transit time of light observed in a stationary state)
- t = The transit time of light observed inside the vehicle
- v = The speed of the vehicle
Special relativity
'Special relativity' is a physics theory that deals with objects moving very fast, such as the speed of light. As velocity increases, some phenomena that classical mechanics cannot explain (Newtonian mechanics) appear. The theory to explain this is 'Special relativity,' perfectly compatible with classical mechanics.
Special relativity started with the idea of Albert Einstein, a famous physicist that everyone knows.
Conditions
Special relativity starts with two conditions:
- In any inertial system, the laws of physics apply equally.
An 'inertial system' refers to a space with no change in speed, such as a train running at a constant speed.
The laws of physics that apply outside the train (law of inertia, F=ma, action-reaction, (angular) momentum, conservation of energy, etc.) also apply equally inside the train. In fact, even assuming the train is stationary and moving is the scenery outside the train, there is no way to figure it out. - The speed of light is the same no matter which inertial system you observe.
Imagine that some light is emitted from a very fast-moving spaceship. If the speed of light observed from the spacecraft is \(c\) and the speed of the spaceship is \(u\), the speed of light observed from the outside is likely to be \(u+c\), but the speed of light is It will still be \(c\). Even if this light is observed in another inertial system, it is still \(c\).
What happens with Special relativity
According to Special relativity, some interesting things happen:
- Time dilation: In an inertial system moving at high speed, time is observed to pass slowly.
- Length contraction: In an inertial system moving at high speed, it is observed that the length of the moving direction axis is shortened.
Time dilation
For an explanation of time dilation, please refer to the link below.
Length contraction
An object moving at a very high speed is measured as a contraction in length.
For example, consider the light emitted from one side of a train is reflected and coming back.
When the train is stationary (or inside the train)
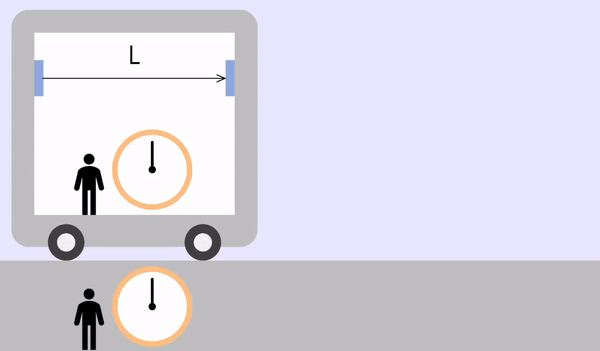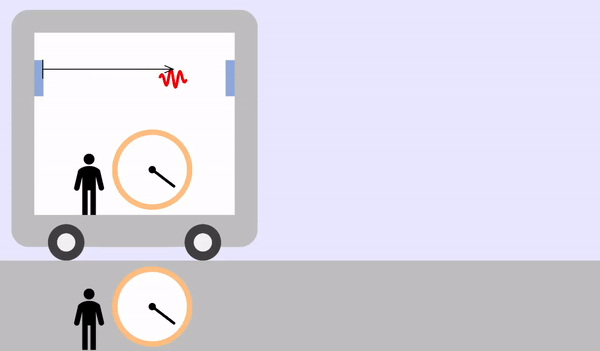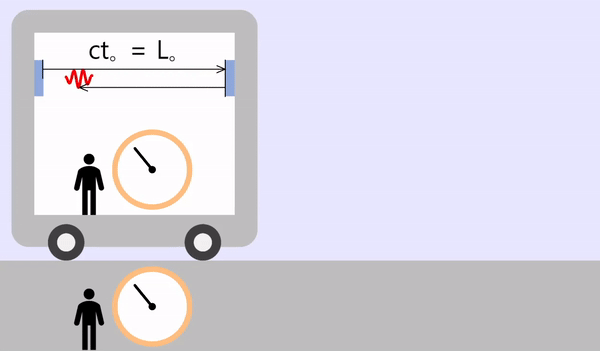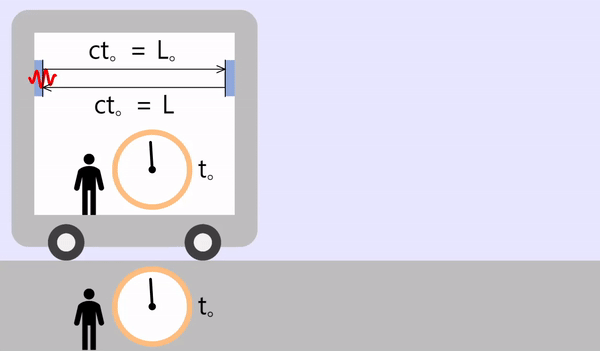
The inside and outside of the train are the same inertial system.
The time to round trip of light is as follows.
\[t_o = \frac{2L_o}{c}\]
If the train is moving with speed \(v\)
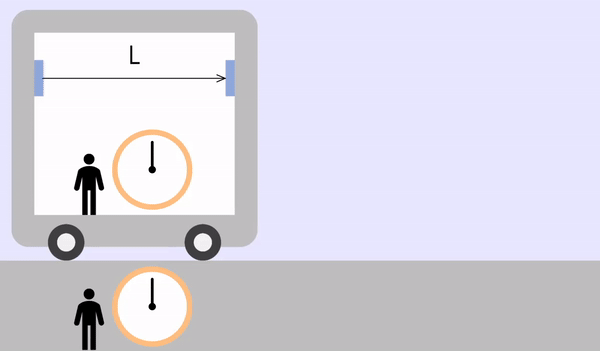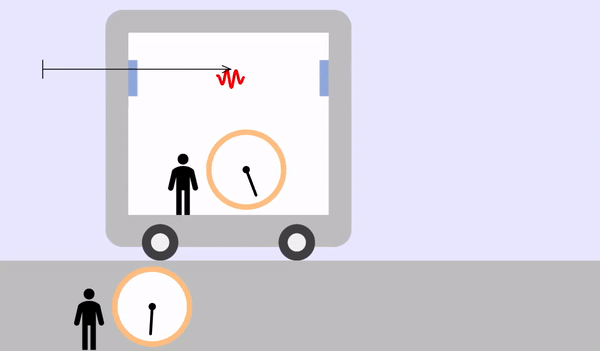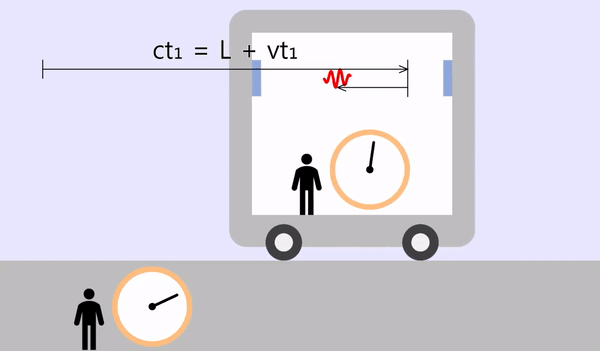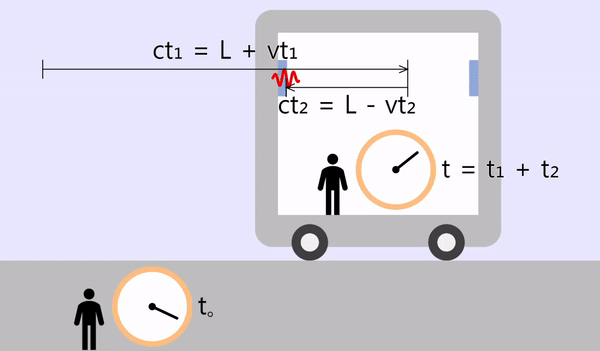
If the time it takes for the light to travel to the right is \(t_1\), the moving distance will be \(L + vt_1\). From the light's point of view, the moving distance is \(ct_1\), and the two values are equal.
\[L + vt_1 = ct_1\\ \color{red}{\therefore t_1 = \frac{L}{c-v}}\]
If the time it takes for the reflected light to travel to the left is \(t_2\), the travel distance will be \(L - vt_2\). The distance traveled by light is \(ct_2\), and the two values are equal.
\[L - vt_2 = ct_2\\ \color{red}{\therefore t_2 = \frac{L}{c+v}}\]
The total time it takes for the light to return is the sum of \(t_1\) and \(t_2\).
\[t = \color{red}{t_1} + \color{red}{t_2} = \frac{L}{c-v} + \frac{L}{c+v} = \frac{2Lc}{c^2 - v^2}\]
The round trip time \(t\) is equal to the time dilation equation \(t = \frac{t_o}{\sqrt{1-\frac{v^2}{c^2}}}\).
\[L = L_O \sqrt{1 - \frac{v^2}{c^2}}\]
As a result, the length of a moving object is always measured contracted.
Also, even the same object is measured with different values depending on who is measuring it.