Young’s Double Slit





 

You can adjust the spacing and position of the slits.

Young’s double slit experiment

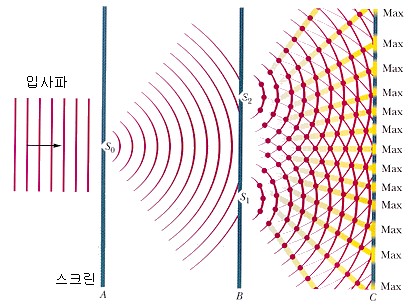
Young’s interference experiment is as follows: The light diffracted from the small holes S0 on-screen ‘A’ passes through the small holes S1 and S2.
Light passing through the two small holes overlaps between screens B and C, creating an interference fringe on screen C.

Constructive interference

When the waves arriving from the two slits are in the same phase, a bright pattern is formed.
To cause constructive interference, the path difference d·sin θ must be ‘0’ or an integer multiple of the wavelength.

Constructive interference \( d\cdot sin(\theta )\,=\,n\lambda \) (n = 0, 1, 2…)

position \( {y }_{ n }\,=\,\frac {n\lambda D }{ d} \) (n = 0, 1, 2…)

d: Slit spacing (m)
θ: diffraction angle (rad)
λ: wavelength of light (m)
D: Distance from slit to screen (m)

When ‘n = 0’, the diffraction angle of the central axis ‘θ = 0’.

Destructive interference

When the waves arriving from the two slits are in the opposite phase, a dark pattern is formed
To cause destructive interference, the difference in the path between the two sources must be an odd multiple of the half wavelength.

Destructive interference \( d\cdot sin(\theta )\,=\,(n+\frac {1 }{ 2} )\lambda \) (n = 0, 1, 2…)

position \( {y }_{ n }\, =\, \frac {\left( n+\frac {1 }{ 2} \right) \lambda D }{ d} \) (n = 0 , 1, 2…)

d: Slit spacing (m)
θ: diffraction angle (rad)
λ: wavelength of light (m)
D: Distance from slit to screen (m)

The ‘n’ value above is used to number dark patterns caused by destructive interference.