Movement of an object suspended from a pulley

Movement on the pulley

Two objects are connected by a string on a fixed, frictionless pulley and are moving together. In this case, the mass of the string and pulley is ignored.

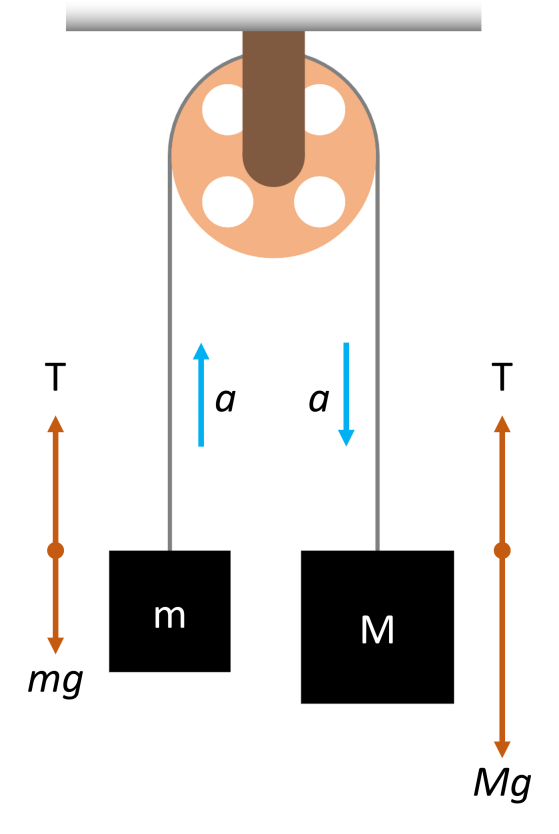
Since tension \(T\) and gravity \(g\) act in opposite directions on an object with mass \(m\) and \(M\), the equation of motion is:
\[T – mg = ma, \quad Mg – T = Ma\]
From the above two equations, the acceleration \(a\), and tension \(T\) of the object can be obtained as:
\[a=\frac{M-m}{M+m}g, \quad T=\frac{2Mm}{M+m}g\]