How cannonball become an artificial satellite?
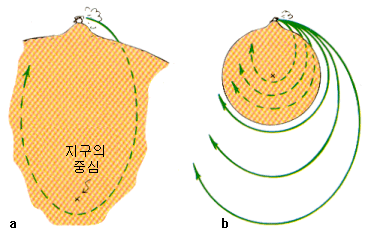
a. Imagine that a cannonball falls in a parabolic curve. The trajectory the cannonball draws is actually part of an elliptical orbit centered around the Earth. The center of the Earth corresponds to the distant focal point of the ellipse.
b. In order for the cannonball to not collide with the surface, it must be fired flush with the surface at a speed of at least 8 km/s (7920 m/s to be exact). If the speed is faster than this, it performs an elliptical motion with the center point of the earth as the ellipse's close focal point.
Satellite thrown by Superman
When Superman throws a stone on a high mountain, a stone has various movements depending on the initial speed.
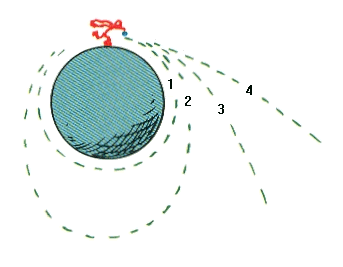
- ≒ 8km/s
The stone goes in a circular orbit in accordance with the curvature of the Earth's surface. However, this is possible only under the assumption that there is no collision with other objects or friction with the atmosphere. The stone will go around the earth in 90 minutes and return to its place. - < 11.2km/s
The stone goes in an elliptical orbit. It takes over 90 minutes to return. - ≒ 11.2km/s
The stone draws a hyperbolic trajectory. If the stone is thrown at a faster speed, the ball will not return again. - > 11.2km/s
Stones can escape the Earth. - > 42.5km/s
Stones can escape the solar system.
A centripetal force, the force that causes the satellite to rotate
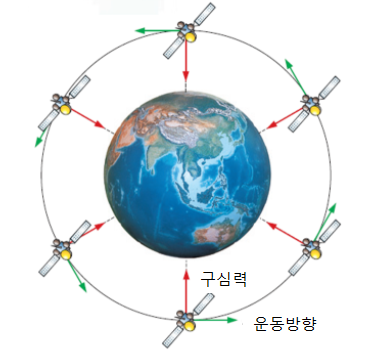
Although it is not visible, there are currently many satellites orbiting on the Earth, and these satellites are moving in a constant orbit around the Earth. Gravity, the force that the Earth pulls on the satellite, becomes the centripetal force.
Calculation of velocity to maintain circular orbit
Think of a satellite in a circular orbit with a radius of r.
If gravity and centripetal force are the same, the satellite is in a circular motion.
\[ \begin{align} ( centripetal force &= gravity ) \\ m\frac { { v }^{ 2 } }{ r } &=G\frac { Mm }{ { r }^{ 2 } } \end{align} \]
Calculation of escape speed
If the satellite's kinetic energy can exceed its potential energy, it will escape from Earth.
\[ \begin{align} ( kinetic energy of satellite &= potential energy ) \\ \frac { 1 }{ 2 } m{ v }^{ 2 }&=G\frac { Mm }{ r } \end{align} \]
The falling moon
The same kind of force that causes the apple to fall from the tree works on the moon.
The moon falls 1.4mm in 1 second due to Earth's gravity.
