Force to move the pendulum

Tension by gravity

In physics, tension is the force on a string connecting two objects. Generally, the tension is calculated from both ends toward the center. When the length of the pendulum is $l$, let’s consider the pendulum raised and released by an angle $\theta_m$. The mass of the string is assumed to be zero.

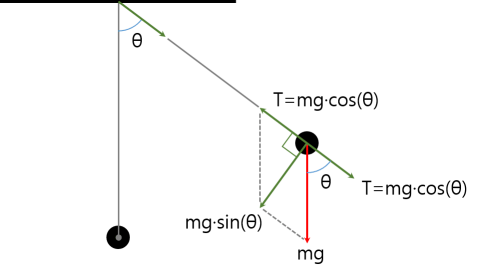
The source of force to move the pendulum is gravity(= $mg$). This gravity can be divided into two forces:

• Tension by gravity, T = $mg\cdot cos\theta$
• The force to moves the pendulum = $mg\cdot sin\theta$ (= Vector sum of ‘T’ and ‘mg’)

Centripetal force of pendulum

When the pendulum descends from the top, one more power is added. It is the centripetal force to maintain the rotational motion of the pendulum.
If the length is $l$ and the speed is $v$, the centripetal force is:

$$F=\frac{mv^2}{l}$$

Like ‘tension by gravity,’ the centripetal force goes from the end to the center.

Total tension applied to the string

The total tension applied to the string can be calculated as follows.

$$\begin{align} The\,total\,tension &= Tension\,by\,gravity \, + \, Centripetal\,force \\&= mg \cdot cos \theta \, + \, \frac{mv^2}{l} \end{align}$$

Let’s make the above expression simple with an expression related to $\theta$.
Consider a pendulum with the highest amplitude $\theta_m$, and the current amplitude $\theta$.

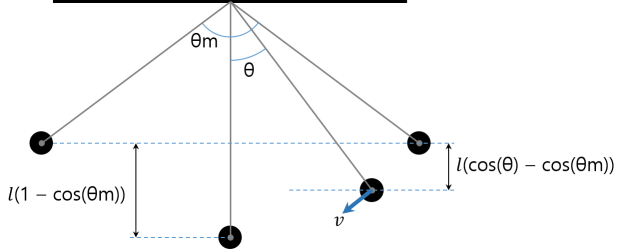
The increased kinetic energy is equal to the reduced potential energy by the law of conservation of energy.

$$\frac{1}{2} mv^2 = mgl(cos \theta – cos \theta_m ) \\ \therefore v^2 = 2gl(cos \theta – cos \theta_m )$$

Substituting the above equation into the total tension, we get:

$$\begin{align} The\,total\,tension &= Tension\,by\,gravity \, + \, Centripetal\,force \\&= mg \cdot cos \theta \, + \, \frac{m \cdot 2gl(cos \theta – cos \theta_m )}{l} \\&= mg \cdot cos \theta \, + \, 2mg(cos \theta – cos \theta_m ) \\&= mg(3cos \theta – 2cos \theta_m ) \end{align}$$