Battery and Load
In an electrical circuit, the battery maintains a voltage difference to allow current to flow through the circuit.
In an electric circuit, the place where energy is consumed is called a load. Generally, in school labs, the load will be a little bulb or a resistor.
In all electrical circuits, the voltage goes down exactly as it goes up. The sum of the ascending and descending heights is ‘0’. Let’s think about a roller coaster. When you ride a roller coaster, it rises to a high place at first. Then, the roller coaster goes down. The roller coaster that passed the track eventually returns to its original position.
Serial connection of resistors
When two resistors are connected in series, each resistor divides the entire voltage. When all the voltages applied to the resistors are added, they become the original voltage.
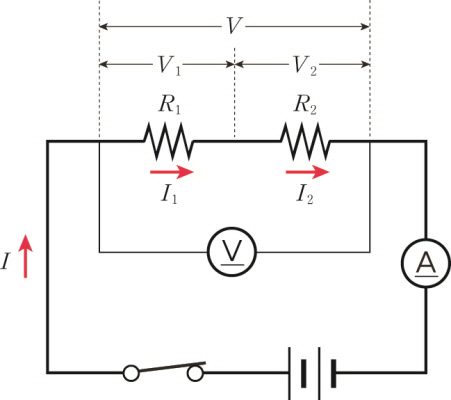
When two or more resistors are connected in series, the current flowing through each resistor is equal to the current flowing through the entire circuit.
\[ I\; =\; { I }_{ 1 } \; = \; { I }_{ 2 } \]
\[ V\; =\; { V }_{ 1 }+{ V }_{ 2 } \]
If the current flowing in the entire circuit is I, V 1 = IR 1 and V 2 = IR 2 from Ohm’s law.
If the circuit’s total resistance is R, the following relation is obtained from Ohm’s law.
\[ V\; =\; { V }_{ 1 }+V_{ 2 }\; =\; I{ R }_{ 1 }+I{ R }_{ 2 }\; =\; I({ R }_{ 1 }+{ R }_{ 2 }) \]
\[ \therefore \; R\; =\; { R }_{ 1 }+{ R }_{ 2 } \]
When two or more resistors are connected in series, the combined resistance equals the resistors’ sum. Therefore, the more the resistors are connected in series, the larger the combined resistance.
Parallel connection of resistors
The voltage applied to each resistor is equal to the original voltage.
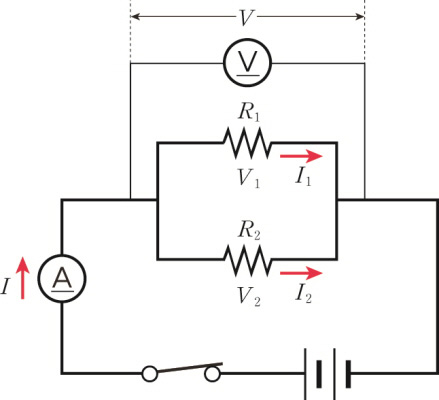
The sum of the currents flowing through each resistor is equal to the current flowing through the entire circuit.
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 } \]
\[ V\; =\; { V }_{ 1 } \; = \;V_{ 2 } \]
From Ohm’s law, The composite current is
\[ I\; =\; { I }_{ 1 }+{ I }_{ 2 }\; =\; \frac { V }{ { R }_{ 1 } } +\frac { V }{ { R }_{ 2 } } \; =\; V(\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } ) \]
And we can get the composite resistor.
\[ \therefore \; \frac { 1 }{ R } \;=\; \frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } \]
Therefore, The more the resistors are connected in parallel, the smaller the combined resistance.