민코프스키 시공간
민코프스키 시공간(Minkowski Spacetime)은 독일수학자 민코프스키가 고안한 좌표계입니다. 특이한 점은 좌표계에 공간(space)뿐만 아니라 시간(time)도 들어있다는 점입니다.
민코프스키 시공간은 수학의 행렬를 사용하여 3차원 공간과 시간을 통합하여 4차원의 좌표계(x, y, z, ct)를 표현합니다. 하지만 4차원 행렬은 매우 복잡하기 때문에, 보통은 한 축(예: x축) 방향의 운동만 다룹니다. 이렇게 하면 가로축은 공간의 x축, 세로축은 시간으로 이루어진 좌표 평면(x, ct)이 됩니다.
민코프스키 시공간을 사용하면 '쌍둥이 역설'과 같은 상대성 이론에 따른 시간 팽창 현상을 쉽게 설명할 수 있습니다.
쌍둥이 역설에 대한 포스팅은 아래 링크를 참고해주세요.
민코프스키 시공간의 이해
민코프스키 시공간을 도입할 때는 다음을 명심해야 합니다.
- 관찰자들은 각자의 좌표계를 기초로 주변의 사물들을 관찰합니다.
- 빛의 속도는 어떤 좌표계에서도 동일합니다.
- 빛의 속도가 동일하기 위해서 좌표계의 축들은 휘어지거나 기울어져 있을 수 있습니다.
예를 들어, 아주 빠른(광속의 절반) 우주선이 지구를 출발하여 등속 운동을 하고 있다고 가정해 보겠습니다.
지구를 기준으로 보면?

파란색 띠는 지구를 기준으로 하는 시간대(time zone)입니다.
지구는 정지해 있고 우주선은 지구로부터 계속 멀어집니다.
이동중인 우주선의 시간은 지구보다 천천히 흐르기 때문에, 늘어난 시간만큼 지구의 시간대로부터 벗어나고 있습니다.
지구와 우주선의 움직임은 아래와 같이 민코프스키 평면상에 점으로 표시할 수 있습니다.
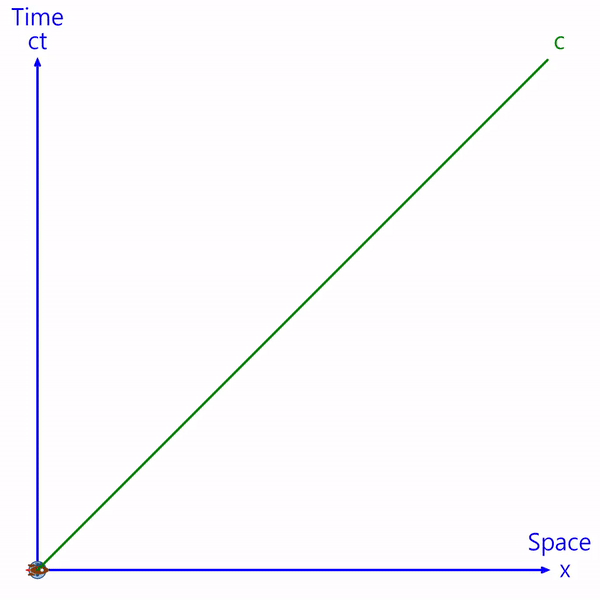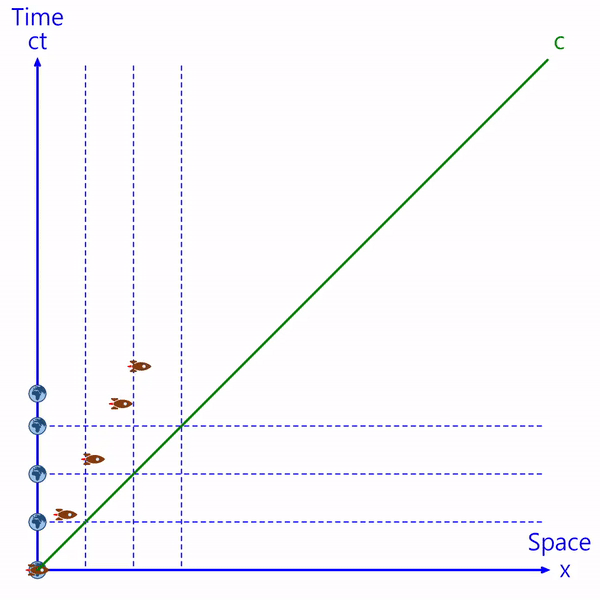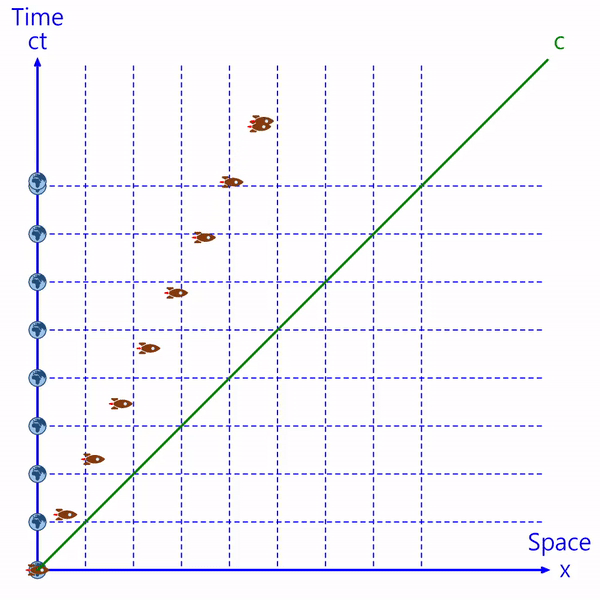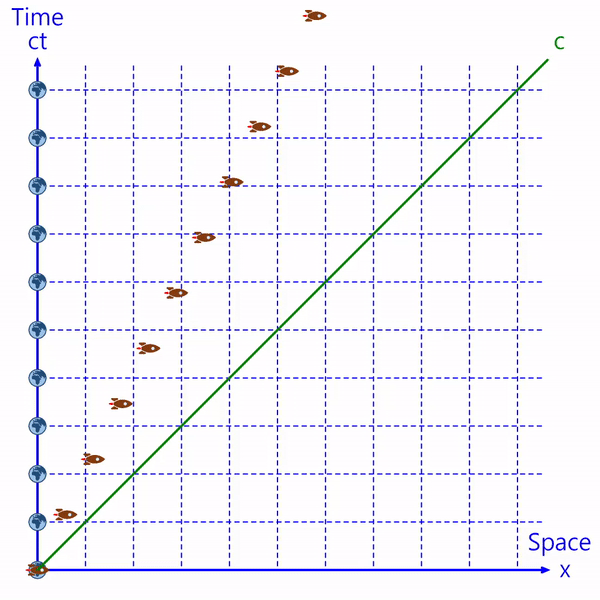
가로축은 물체가 위치한 공간을 나타내고, 세로축은 물체의 시간을 나타냅니다. (세로축은 시간에 빛의 속력을 곱해서 'ct'로 표시합니다. 허수를 포함하여 'ict'로 표시하기도 합니다.)
지구를 기준으로 생각하면 지구는 정지해 있으므로, 지구는 시간축 위에 위치합니다.
모든 물체의 속력은 빛보다 빠를 수 없으므로, 시공간 상에서 우주선의 위치는 빛의 속력을 나타내는 직선(c)보다 왼쪽에 있습니다.
우주선을 기준으로 하면?
우주선을 기준으로 하는 좌표계는 어떤 모습일까요?
우주선을 기준으로 한다는 것은 위치가 항상 '0'이라는 뜻입니다. 즉, 우주선은 시간축(ct') 상에 위치합니다.
우주선을 기준으로 하면 빛의 속도는 어떻게 바뀔까요?
특수 상대성 이론에 따르면, 좌표계가 달라지는 경우에도 빛의 속도는 변화가 없습니다. 다시 말하자면, 광속의 기울기(c)는 일정합니다.
시간축(ct')이 기울어진 좌표계에서 광속의 기울기를 일정하게 유지하기 위해서는 공간축(x')도 기울어져야 합니다.

따라서 우주선을 기준으로 하는 시공간 좌표계는 아래와 같이 변형됩니다.(빨간색)

두 좌표계를 겹쳐 보면 아래와 같습니다.
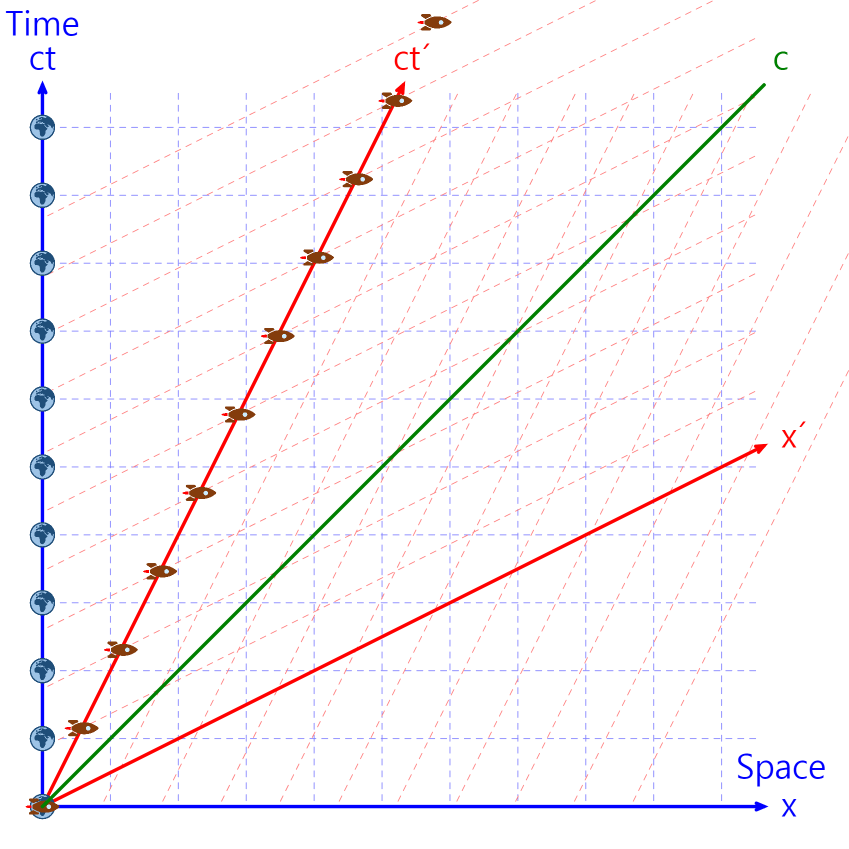
파란색 점선은 지구를 기준으로 한 좌표계, 빨간색 점선은 우주선을 기준으로 한 좌표계입니다.
위 그래프는 다음의 현상들을 설명하고 있습니다.
- 지구와 우주선은 각자의 좌표계에서 시간축에 위치한다. 즉, 정지해 있다.
- 빛의 속력은 좌표계와 상관없이 어디서나 일정하다.
- 지구와 우주선은 각각 상대편의 시간이 천천히 흐르는 것처럼 보인다.
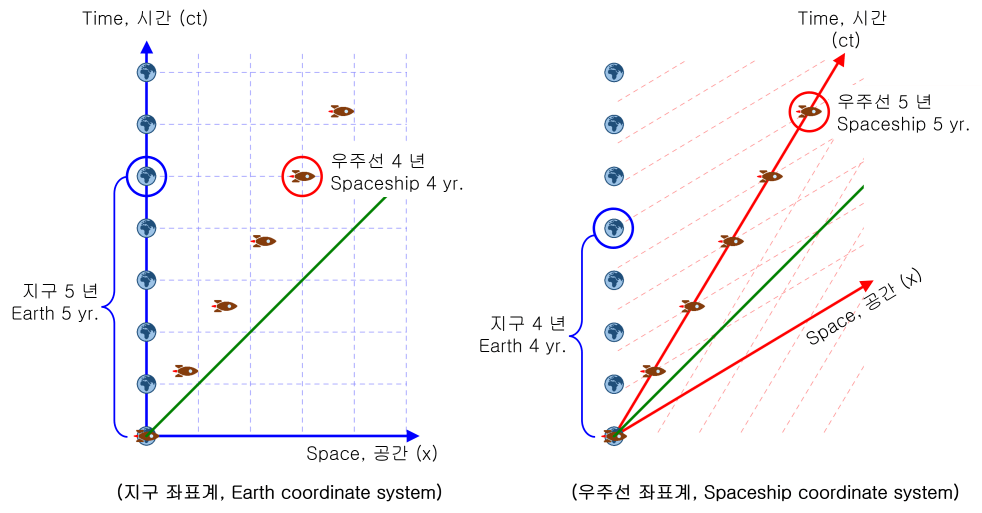
위 그림은 우주선이 광속의 0.6배로 지구로부터 멀어지는 것을 나타낸 것입니다. 두 그림은 서로 같은 운동이며, 좌표계만 다르게 관찰한 것입니다.
지구 중심 좌표계로 보면 우주선의 시간이 천천히 흐르고 있습니다.
그런데, 우주선 중심 좌표계로 보면 지구의 시간이 천천히 흐르는 것으로 보입니다.
이것은 각자의 좌표계를 통해 상대편을 관찰하기 때문입니다.