이 시뮬레이션에서 사용된 기호의 뜻은 다음과 같습니다.
- L = 정지 상태에서 빛이 이동하는 거리, ('거리 = 속력×시간'이므로 'ct。'와 같음)
- c = 빛의 속력 (≒ 299,792,458 m/s)
- t。 = 우주선 내부에서 관찰한 빛의 이동 시간(또는 정지 상태에서 관찰한 빛의 이동 시간)
- t = 우주선 외부에서 관찰한 빛의 이동 시간
- v = 우주선의 속력
특수 상대성 이론
특수 상대성 이론은 빛의 속도와 같이 매우 빨리 이동하는 물체를 다루는 물리 이론입니다. 물체의 속도가 증가하면, 고전 역학(뉴턴 역학)으로 설명할 수 없는 현상들이 나타납니다. 이를 설명하기 위한 이론이 특수 상대성 이론이며, 고전 역학과 완벽하게 호환됩니다.
특수 상대성 이론은 누구나 알고 있는 유명한 물리학자, 알버트 아인슈타인의 아이디어입니다.
가정
특수 상대성 이론은 다음과 같은 두 개의 가정으로부터 시작됩니다.
- 어느 관성계에서도 물리 법칙은 동등하게 적용됩니다.
'관성계'는 일정한 속도로 달리는 열차와 같이 속도의 변화가 없는 공간을 말합니다.
열차 밖에서 적용되는 물리 법칙들(관성의 법칙, F=ma, 작용-반작용, (각)운동량 및 에너지 보존 법칙들)은 열차 안에서도 동등하게 적용됩니다. 사실, 열차는 정지해 있고, 이동하는 것은 열차 밖 풍경이라고 가정하더라도 이를 구분할 방법은 없습니다. - 어느 관성계에서 관측하든지 빛의 속도는 동일하게 관측됩니다.
아주 빨리 움직이는 우주선으로부터 어떤 빛이 방출되었다고 생각해 봅시다. 우주선에서 관측한 빛의 속도를 \(c\)라고 하고, 우주선의 속도를 \(u\)라고 하면, 외부에서 관측한 빛의 속도는 \(u+c\)일것 같지만, 빛의 속도는 여전히 \(c\)가 됩니다. 이 빛은 어떤 관성계의 또 다른 관찰자가 관측한다고 해도, 여전히 \(c\)입니다.
특수 상대성 이론으로 인해 일어나는 일들
특수 상대성 이론에 따르면 다음과 같은 재미있는 일들이 일어납니다.
- 시간 팽창: 빠른 속도로 움직이는 관성계는 시간이 천천히 흐르는 것으로 관측됩니다.
- 길이 수축: 빠른 속도로 움직이는 관성계는 이동하는 방향축의 길이가 짧아진 것으로 관측됩니다.
시간 팽창(시간 지연)
빠른 속도로 이동중인 물체 내부의 시간은 천천히 흐릅니다.
물론 모든 관성계는 동등하기 때문에, 우주선의 입장에서 바깥 우주를 본다면, 바깥 우주의 시간이 천천히 흐르는 것으로 관측됩니다.
아주 빠른 속도로 이동하고 있는 우주선이 있다고 가정해 봅시다.
우주선이 정지해 있는 경우
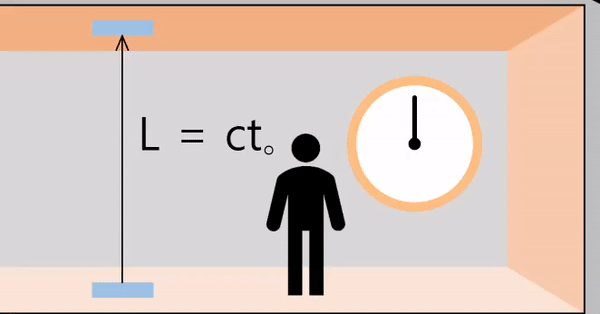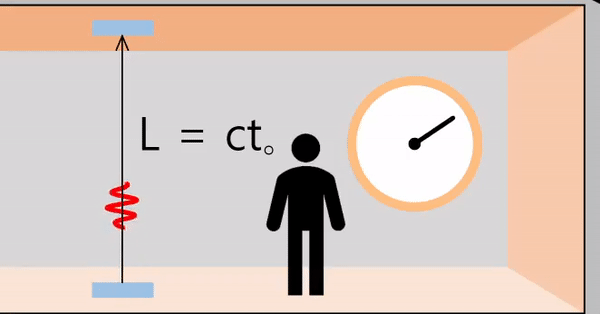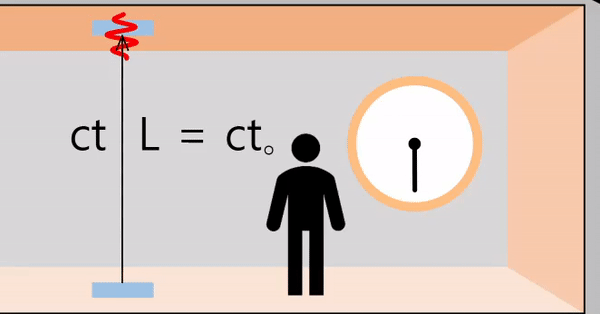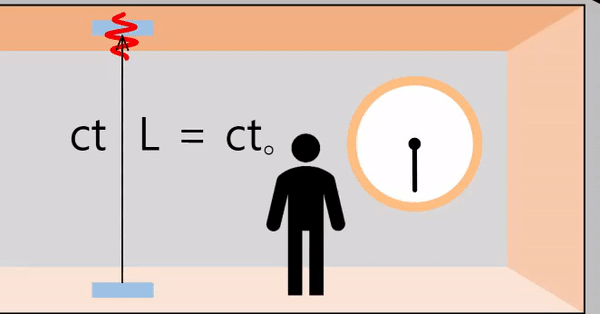
우주선 안과 바깥이 동일한 관성계입니다.
우주선의 바닥에서 방출된 빛이 천정까지 이동한다고 가정합시다. '거리 = (빛의)속력 × 시간'이므로, 다음의 공식이 성립합니다.
\[L = ct_o\]
우주선이 속력 \(v\)로 움직이는 경우

내부 관찰자가 보았을 때, 우주선 바닥에서 방출된 빛이 천정까지 이동하는데 걸리는 시간 및 거리는 우주선이 정지했던 경우와 동일합니다(우주선의 이동 방향과 관계없는 수직 방향).
\(t_o\)는 우주선 내부 관찰자가 관측한 시간입니다.
\[L = ct_o\]
외부에서 보았을 때는, 우주선이 \(v\)의 속도로 이동하고 있으므로 빛은 빗변과 같은 경로로 이동하며 이동거리는 다음과 같이 구할 수 있습니다.
\(t\)는 외부에서 관측한 시간입니다.
\[빗변 = ct\]
외부에서 보는 우주선의 이동 거리는 \(vt\)이므로, 피타고라스 원리에 의해 다음의 식이 성립합니다.
\[{(ct)}^2 = {(ct_o)}^2 + {(vt)}^2\]
위 식을 \(t\)에 대해 풀면 다음과 같습니다.
\[t = \frac{t_o}{\sqrt{1-\frac{v^2}{c^2}}}\]
\(v\)가 0이 아니라면, \(t\)는 \(t_o\)보다 항상 깁니다. 즉, 움직이는 관성계의 시간은 팽창됩니다.
일상생활에서의 속력은 빛보다 훨씬 느립니다. 그래서, 일상생활에서 시간이 지연되는 효과는 거의 '0'입니다.
길이 수축
길이 수축에 대한 설명은 아래 링크를 참고 바랍니다.