지구에서 사용하던 저울을 이용하여, 다른 행성에서의 내 몸무게를 측정해 봅시다.
중력을 수학적으로 설명한 뉴턴
모든 물체는 주변에 중력장이 있어서 주변의 물체들을 끌어 당기고 있습니다. 이 중력장의 크기는 물체의 질량과 비례합니다.

중력의 개념은 영국의 뉴턴이 처음으로 제안한 것입니다. 전염병이 돌아 학교가 휴교를 하자, 뉴턴은 영국의 고향으로 돌아와 사과나무 밑에서 중력의 법칙을 발견한 것으로 알려져 있습니다. 그런데, 정말로 그랬는지는 확실치 않습니다. (앞으로도 그럴 것이지만 상당히 많은 이야기들은 지어진 경우가 많습니다. 세상에 믿을 것은 여러분의 건전한 사고력 밖에 없습니다!)
그러면, 뉴턴이 발견한 중력을 공식으로 알아보겠습니다. 뉴턴의 중력은 다음과 같이 표현할 수 있습니다.
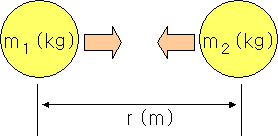
\[F=G\frac { { m }_{ 1 }{ m }_{ 2 } }{ { r }^{ 2 } } \]
질량을 가진 두 물체는 서로 잡아당깁니다. 그 힘은 물체의 질량에 비례하고 두 물체 사이의 거리의 제곱에 반비례합니다. 'F'는 힘으로서 단위는 'N(뉴튼)'입니다.
G값은 비례상수로서 정밀한 실험 결과 밝혀진 값입니다.
즉, 1 kg 의 두 물체가 1 m 만큼 떨어져 있으면 약 6.67 x 10-11 N의 힘으로 잡아당기는 것입니다. G의 값이 매우 작으므로 우리는 중력이 매우 약한 힘이라는 것을 알 수 있습니다. 다시 말하지만, 중력은 현재까지 알려진 네 개의 기본 힘들 중 가장 약한 힘입니다. 하지만 전 우주에 걸쳐 가장 득세한 힘이기도 합니다.
지구와 같은 큰 물체는 큰 중력장을 낼 수 있지만, 주변의 작은 물체들은 서로 잡아당길 만한 큰 중력을 낼 수 없습니다. 따라서 우리 주변에서 볼 수 있는 대부분의 중력은 지구가 잡아당기는 힘입니다.