地球上で使用したスケールで、いくつかの惑星の私の体重を測定しましょう。
重力を数学的に説明したニュートン
すべての物体は、周囲に重力場があって周辺の物体を引きつけています。この重力場の強さは、物体の質量に比例します。

重力の概念は、英国のニュートンが初めて提案したものです。伝染病が流行して学校が休校をすると、ニュートンは、英国の故郷に戻ってきたあと、リンゴの木の下で、重力の法則を発見したことが知られています。ところで、本当にやったのはっきりしません。(今後もそうだが、かなり多くの話は建てられた場合があります。世の中に信頼はあなたの健全な思考力しかありません!)
それでは、ニュートンが発見した重力を公式に説明します。ニュートンの重力は、次のように表現することができます。
\[F=G\frac { { m }_{ 1 }{ m }_{ 2 } }{ { r }^{ 2 } } \]
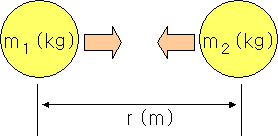
質量を持つ二つの物体は常に引きつけています。その力は、物体の質量の積に比例して、二つの物体間の距離の二乗に反比例します。「F」は力としての単位は「N(ニュートン)」です。
「G」の値は、比例定数として正確な実験結果明らかになった値です。
つまり、1kgの二つの物体が1mほど離れていると、約6.67 x10-11 Nの力で引きつけています。「G」の値が非常に小さいので、私たちは、重力が非常に弱い力であることを知ることができます。重力は、現在までに知られている4つの力中で最も弱い力です。しかし、宇宙で最も勢力を伸ばした力でもあります。
地球のような大きな物体は大きな重力場を出すことができますが、周辺の小さな物体は互いに引きつけるほど大きな重力を出すことができません。したがって、私たちの周りで見ることができるほとんどの重力は地球の引力です。