気体分子の根二乗平均速度（Vrms）

* 上記シミュレーションの気体分子はすべて同じ種類であり、分子の色は単に識別のためのものです。

気体分子運動論

気体分子運動論は気体分子の運動を説明するための仮説です。この仮説を説明するために、次のような仮定を満足させる理想気体を仮定します。 (위키백과)

気体分子は、質量は存在するが、体積はありません。
気体分子は、互いに力を与えられない。
気体分子が起こすすべての衝突は完全弾性衝突である。
気体は、任意の温度や圧力にも決して液化または昇華されない。
気体分子の平均分子運動エネルギーは絶対温度のみ比例し、分子の大きさ、形状、種類には影響を受けない。

気体分子の根二乗平均速度

壁の断面積が $A$ であり、長さが $L$ である箱の中に質量が $m$ である気体粒子が含まれています。

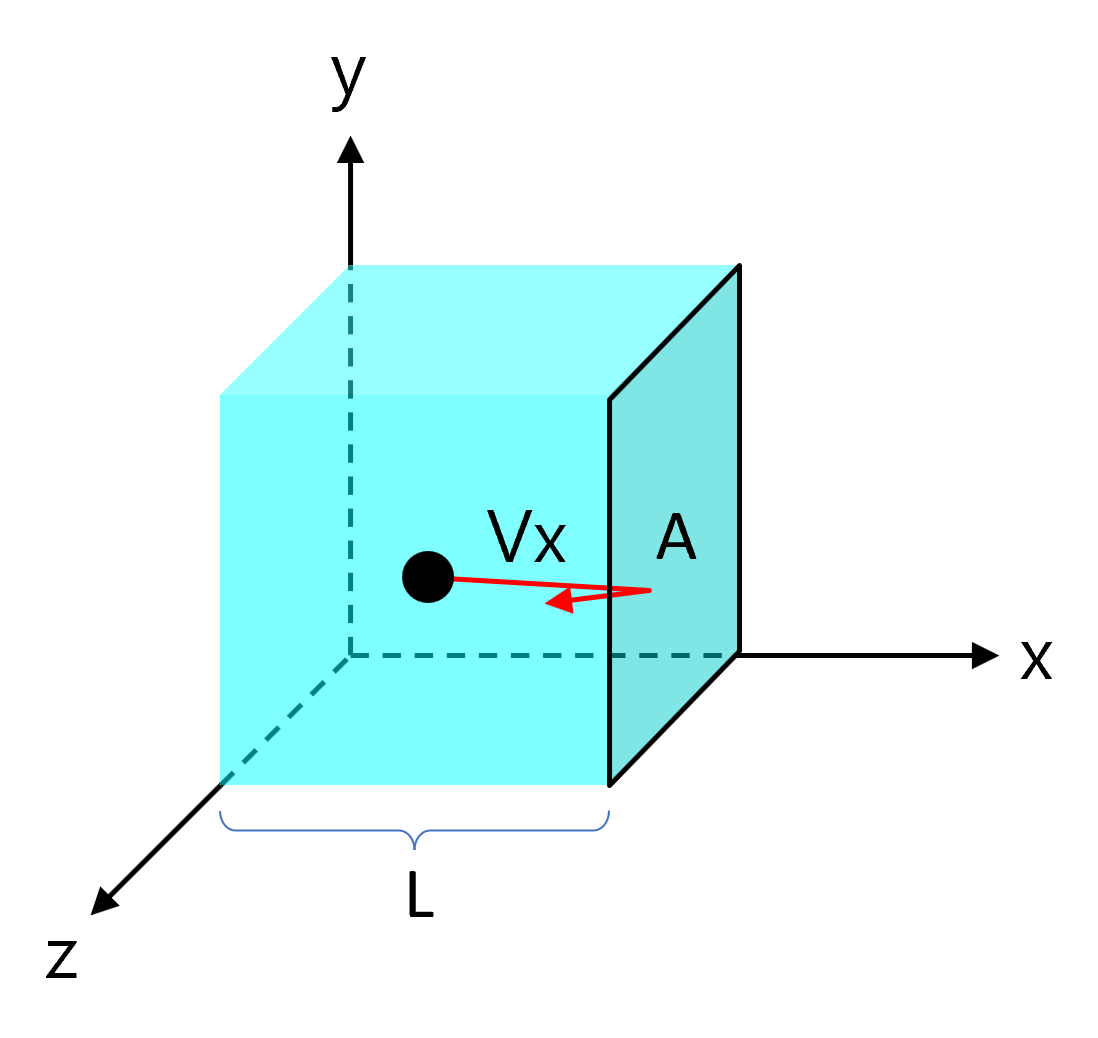
気体粒子は壁と完全弾性衝突し、 $x$ 、 $y$ 、 $z$ 軸方向に無秩序な直線運動をしています。
気体粒子が $v_x$ の速度を持って箱の $A$ 面と衝突する場合を考えてみましょう。壁面 $A$ に影響を与える運動は $x$ 軸成分だけなので、利便性のためにしばらく $y$ 軸と $z$ 軸は思わない。
気体粒子は壁面 $A$ と完全弾性衝突をします。衝突前後の粒子の運動量は、次のように変わります。

$\Delta P_x = mv_x – (-mv_x) = 2mv_x$

気体分子が箱の $A$ 壁面と衝突した後、反対側の壁面と衝突して、再び $A$ 壁面を衝突するの時間は、次のとおりです。

$\Delta t = \frac{2L}{v_x}$

気体分子が毎秒壁面 $A$ に加える衝撃力 $F$ は、運動量の変化量を時間で分けて入手することができます。

$F = \frac {\Delta p}{\Delta t} = \frac {2mv_x}{\frac{2L}{v_x}} = \frac{mv_{x}^{2}}{L}$

壁面 $A$ に加わる圧力 $P$ は、単位面積当力として定義されるので、気体の圧力は、次のとおりです。（体積 $V = AL$ ）

$P = \frac{F}{A} = \frac{\frac{mv_x^2}{L}}{A} = \frac{mv_x^2}{AL} = \frac{mv_x^2}{V}$

気体分子が2個以上の場合、気体分子が壁面 $A$ に加える圧力 $P$ の大きさは、次のとおりです。

$\begin{align} P &= \frac{mv_{x1}^2}{V} + \frac{mv_{x2}^2}{V} + \frac{mv_{x3}^2}{V} \cdots\\ &= \frac{m(v_{x1}^2 + v_{x2}^2 + v_{x3}^2 \cdots )}{V} \\ &= \frac{mN \overline{v_x^2}}{V} \end{align}$

$N$ = 気体分子の数
$\overline{v_x^2}$ = 粒子の $x$ 軸方向速度の二乗の平均値

パスカルの原理に沿って、気体の圧力は、すべての壁に渡って均一に適用されます。
したがって、上で求めた圧力 $P$ は、単に壁面 $A$ のみ該当するものではなく、箱全体の壁にも同様に適用されます。

さて、 $y$ 軸と $z$ 軸方向を考慮してみましょう。気体粒子の速度の二乗（ $v_{rms}^{2}$ ）の平均は、ピタゴラスの定理として表すことができます。

$\overline{v_{rms}^2} = \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2}$

理想気体分子の運動では、すべての軸で同じ自由度を持つため、次のように簡単に考えることができます。

$\overline{v_{rms}^2} = 3\overline{v_x^2} \\ \therefore \overline{v_x^2} = \frac{1}{3}\overline{v_{rms}^2}$

したがって、箱の全体に加わる圧力は、次のとおりです。

$P = \frac{1}{3} \frac{mNv_{rms}^2}{V}$

気体粒子の全質量 $mN$ は、 $nM$ （=没収（ $n$ ）×モル質量（ $M$ ））としても表すことができます。

$P = \frac{1}{3} \frac{nMv_{rms}^2}{V} \\ \therefore PV = \frac{1}{3} nMv_{rms}^2$

上記の結果は、理想気体の状態方程式（ $PV= nRT$ ）と一致する必要があります。

$(PV=\,)\:\:\:\: \frac{1}{3} nMv_{rms}^2 = nRT$

上記の式から二乗平均速度（ $v_{rms}^2$ ）は、絶対温度 $T$ に比例し、モル質量（ $M$ ）に反比例することを知ることができます。

$\overline{v_{rms}^2} = \frac{3RT}{M}$

根二乗平均速度（ $v_{rms}$ ）は、二乗平均速度（ $v_{rms}^2$ ）に平方根をとったものです。

$v_{rms} = \sqrt {\frac{3RT}{M}}$

このように根二乗平均速度は、分子の種類や温度による関数として明確に定義することができ、一定の条件の下で、その値が変動していません。

気体分子の平均速度

平均速度は、気体分子の速度を算術平均として計算した値です。二分子が衝突したときに、運動量は保存されるが、平均速度はずっと変わります。気体粒子の数が十分に多いと仮定した平均速度 < $v$ >は、次のとおりです。（Maxwell-Boltzmann確率分布式から誘導、誘導過程は省略）

$< v > = \sqrt {\frac{8RT}{\pi M}}$

平均速度 < $v$ >は、根二乗平均速度 $v_{rms}$ よりも少し小さい値を持ちます。
そして、平均速度は一定の値を維持していない、少しずつ変化します。分子の数が少なくなるほど変動が激しくなります。