삼각함수의 정의
다음과 같은 직각삼각형이 있다고 생각해 봅니다.
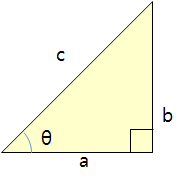
직각삼각형의 가장 긴 변 c는 빗변이 되고, a는 밑변, b는 높이가 됩니다. a와 c가 이루는 각도를 θ라고 가정할 수 있습니다.
여기서 고전적인 삼각함수의 정의는 다음과 같습니다.
sin은 ‘사인’, cos은 ‘코사인’, tan은 ‘탄젠트’로 부릅니다.
‘삼각함수’라는 단어에서 유추할 수 있듯이 삼각함수는 삼각형에서 비롯된 단어입니다. 따라서 삼각함수는 삼각형과 가장 밀접하게 관련이 있을 것 같고, 오직 삼각형 모양에서만 그 의미를 가질 것 같아 보입니다.
하지만, 실제로 삼각함수는 각도에 따른 x축 성분과 y축 성분의 값으로 이해하는 것이 더 중요합니다.
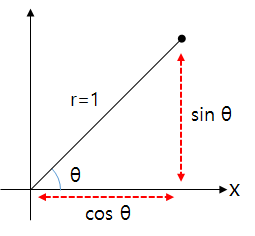
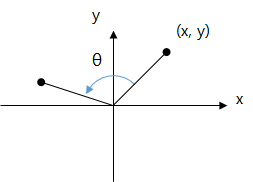
예를 들어 2차원 좌표평면에서 길이가 ‘1’인 선분이 있다고 가정해 봅시다. 이 선분이 x축과 이루는 각도가 θ라면, 선분의 끝 부분 (x, y) 좌표값은 각각 (cos(θ), sin(θ))가 됩니다.
만약 선분의 길이가 변수 ‘r’이라면 선분의 끝 부분 (x, y) 좌표값은 각각 (r·cos(θ), r·sin(θ))가 됩니다.
삼각함수의 응용
이 자바실험실을 만드는 과정에서도 수많은 삼각함수들이 사용되었습니다.
예를 들어 화면상의 물체를 회전시키거나 원운동시켜야 할 때, 사용자가 보기에는 그냥 회전하거나 원운동하는 것으로 보이지만, 화면상의 정확한 위치를 잡기 위해서는 반드시 삼각함수의 도움을 받아야 합니다.
예를 들어 반지름이 r인 한 점이 x축 상에 있다고 가정해 봅시다.
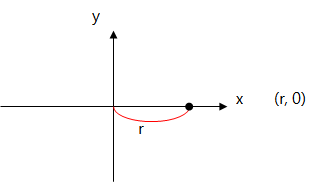
2차원 좌표상에서 이 점의 위치는 (r, θ)로 표시할 수 있습니다.
원점을 기준으로 하여 이 점을 각도 θ 만큼 회전시킨다면 이 점의 좌표는 다음과 같습니다.
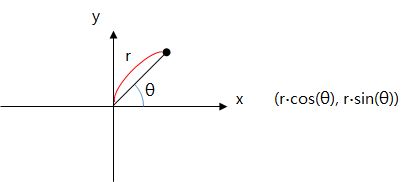
y = r·sin(θ)
이 공식은 회전하는 하는 모든 경우에 유용하게 사용됩니다.
또 다른 예로, 2차원 좌표 (x, y)위치한 점을 각도 θ 만큼 회전시키려면 어떻게 할까요?
회전 변환된 좌표를 (x’, y’)이라고 하면 다음과 같이 구할 수 있습니다.
y’ = x·sin(θ) + y·cos(θ)