수소의 스펙트럼
러더퍼드(Rutherford)가 실험하는 시기에 화학자들은 분광기를 이용하여 화학성분을 분석했고, 물리학자들은 복잡한 스펙트럼 선에서 어떠한 질서를 찾으려고 노력하고 있었습니다.
예를 들어, 가벼운 원소인 수소를 넣은 수소 방전관은 다른 원소에 비해 매우 질서 정연한 스펙트럼을 나타냅니다.
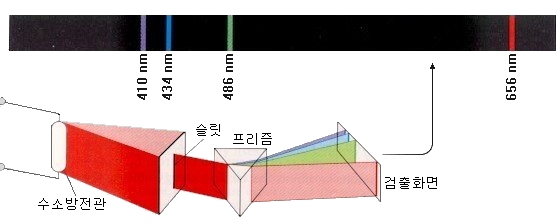
적색 영역에 선이 한 개, 청록색 영역에 선이 한 개, 보라색 영역에 몇개의 선이 있고 자외선 영역에는 선이 많은 것이 수소원자의 스펙트럼입니다. 자외선 영역의 빛은 우리 눈에 보이지 않습니다.
수소 원자 스펙트럼내에 나타나는 파장들이 분명하게 구분되는 모임들로 구성되어 있다는 것은 19세기말에 이미 발견되었습니다.
스위스의 교사였던 Balmer는 이 스펙트럼 선의 위치를 간단한 수학적 공식으로 나타내었지만 그 자신도 이 공식이 왜 잘 맞는가를 이해하지 못했습니다. 이 공식을 이용하면 아직 발견하지 못한 선까지 예측할 수 있었습니다.
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 2 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=3,4,5… \]
λ = 빛의 파장(nm)
R = Rydberg상수( ≒ 1.097×107m-1)
R은 전자가 무한대의 위치에 있다고 가정한 전자의 위치 에너지값으로서 뤼드베리 상수라고 합니다.
양자도약
원자 속의 전자는 에너지를 흡수하여 높은 궤도로 올라설 수 있습니다.
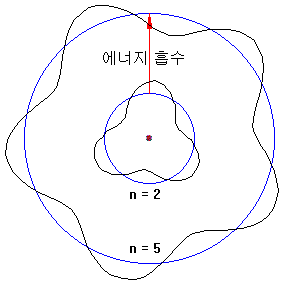
에너지를 얻는 방법들은 다음과 같습니다.
- 다른 원자들과 충돌하여 운동에너지의 일부분을 흡수
- 자유전자들과 충돌하여 전자의 운동에너지를 얻음
- 적당한 에너지를 가진 빛(광자)을 흡수
반대로, 높은 궤도의 전자는 에너지를 방출하면서 낮은 궤도로 떨어질 수 있습니다(예: 5 → 2). 이때, 에너지는 빛(광자)의 형태로 방출됩니다.
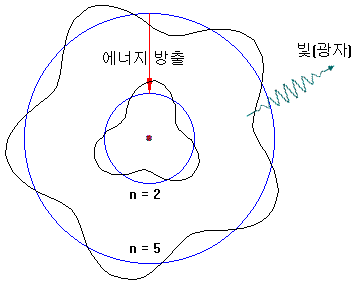
전자 궤도는 정수값만 존재하고 그 사이에는 있을 수 없습니다. 예를들어, n = 3.2 는 될 수 없습니다.
따라서, 특정한 파장의 스펙트럼만 관찰됩니다.
스펙트럼 계열
전자가 어디까지 떨어지는가에 따라 방출하는 빛의 파장이 달라집니다.
- Lyman 계열: 높은 준위의 전자가 n=1인 바닥상태로 떨어질 때 방출하는 빛의 파장
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 1 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=2,3,4… \] - Balmer 계열: 높은 준위의 전자가 n=2 상태로 떨어질 때 방출하는 빛의 파장
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 2 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=3,4,5… \] - Paschen 계열: 높은 준위의 전자가 n=3 상태로 떨어질 때 방출하는 빛의 파장
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=4,5,6… \] - Brackett 계열: 높은 준위의 전자가 n=4 상태로 떨어질 때 방출하는 빛의 파장
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 4 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=5,6,7… \]
λ = 빛의 파장(nm)
R = Rydberg상수( ≒ 1.097×107m-1)