三角関数の定義
次のような直角三角形があると考えましょう。
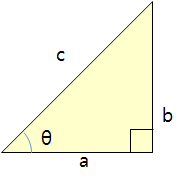
直角三角形の最も長い辺「c」は、斜辺となり、「a」は、下辺、「b」は、高さになります。「a」と「c」との間の角度を「θ」と仮定することができます。
ここで、古典的な三角関数の定義は次のとおりです。
sinは「サイン」、cosは「コサイン」、tanは「タンジェント」と呼びます。
「三角関数」という言葉から推測することができるように、三角関数は三角形で始まった言葉です。したがって、三角関数は三角形と最も密接に関連しているようで、唯一の三角形だけその意味を持つように見えます。
しかし、実際には、三角関数は角度に応じた「x」軸成分と「y」軸成分の値として理解することが重要です。
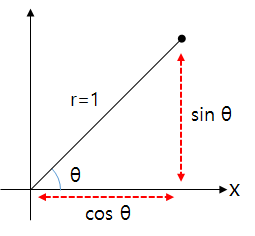
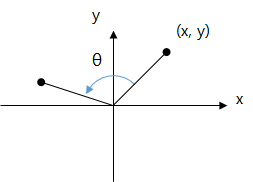
たとえば、2次元の座標平面での長さが「1」である線分があるとしましょう。この線分と「x」軸との間の角度が「θ」であれば、線分の端(x、y)座標値は、それぞれ(cos(θ)、sin(θ))となります。
もし線分の長さが変数「r」であれば、線分の端(x、y)座標値は、それぞれ(r・cos(θ)、r・sin(θ))となります。
三角関数の応用
この「Javaの実験室」を作る過程でも多くの三角関数が使用されています。
例えば、画面上の物体を回転させたり、円運動させるときに、画面上の正確な位置をとるためには、三角関数を利用します。
例えば、半径が「r」であるした点が「x」軸上にあると仮定してみましょう。
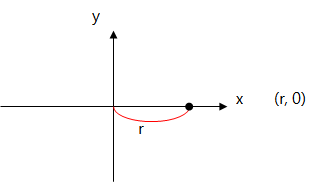
2次元の座標上で、この点の位置は、(r、θ)で表示することができます。
原点を基準にして、この点を角度「θ」だけ回転させると、この点の座標は、次のとおりです。
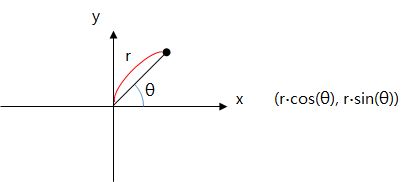
y = r·sin(θ)
この公式は、回転するすべての場合に便利です。
別の例として、2次元座標(x、y)位置点を角度「θ」だけ回転させるにはどうしましょう?
回転変換された座標を(x’、y’)とすると、次のように求めることができます。
y’ = x·sin(θ) + y·cos(θ)