水素原子のスペクトル

水素のスペクトル

ラザフォード（Rutherford）が実験する時期に、化学者たちは分光器を利用して化学成分を分析し、物理学者たちは、複雑なスペクトル線の中でどのような秩序を見つけようとしました。
例えば、軽い元素である水素を入れた水素放電管は、他の元素に比べて非常に秩序あるスペクトルを示します。

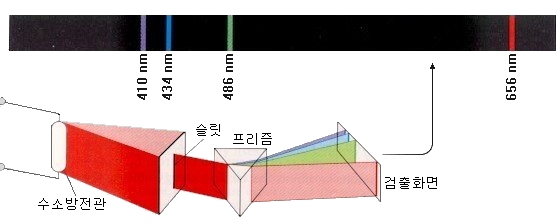
赤色領域に線が1本、シアン領域に線が1本、紫の領域にいくつかの線があり、紫外線領域に線が多いのが、水素原子のスペクトルです。紫外線領域の光は、私たちの目には見えません。

水素原子のスペクトルに現れる波長が明らかに区分されている会で構成されているということは、19世紀末にすでに発見されました。
スイス教師だったBalmerはスペクトル線の位置を数学的な公式に示しました。しかし、自分もこの公式がなぜ成立するかを理解していませんでした。この方式を利用すれば、まだ発見していない線まで予測することができました。

\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 2 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=3,4,5… \]

λ = 光の波長（nm）
R = リュードベリ（Rydberg）定数（ ≒ 1.097×10⁷m^-1）
「R」は、電子が無限大の位置にあると仮定した電子の位置エネルギーの値として、「リュードベリ（Rydberg）定数」といいます。

量子跳躍

原子の中の電子はエネルギーを吸収し、高い軌道に立ち上がることができます。

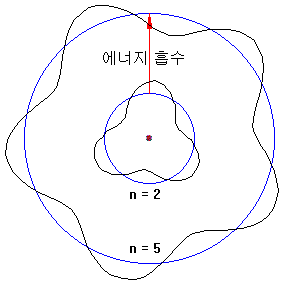
エネルギーを得る方法は、次のとおりです。

他の原子と衝突して運動エネルギーの一部を吸収
自由電子と衝突して電子の運動エネルギーを得る
適切なエネルギーの光を吸収

逆に、高い軌道の電子はエネルギーを放出しながら、低軌道に落ちることができます（例：5→2）。このとき、エネルギーは光の形で放出されます。

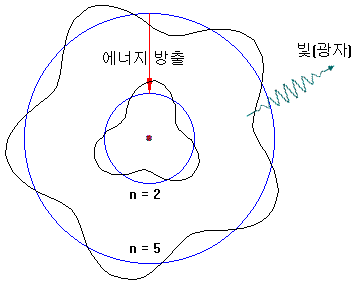
電子軌道は、整数値のみが存在し、その間には、電子が存在することができません。例えば、n=3.2はできません。
したがって、特定の波長のスペクトルのみ観察されます。

スペクトル系列

電子がどこまで落ちるに応じて放出する光の波長が異なります。

Lyman系列：高レベルの電子が「n=1」である基底状態に落ちるとき、放出する光の波長
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 1 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=2,3,4… \]
Balmer系列：高レベルの電子が「n=2」の状態に落ちるとき、放出する光の波長
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 2 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=3,4,5… \]
Paschen系列：高レベルの電子が「n=3」の状態に落ちるとき、放出する光の波長
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 3 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=4,5,6… \]
Brackett系列：高レベルの電子が「n=4」の状態に落ちるとき、放出する光の波長
\[ \frac { 1 }{ \lambda } =R(\frac { 1 }{ { 4 }^{ 2 } } -\frac { 1 }{ { n }^{ 2 } } )\quad \quad \quad n=5,6,7… \]

λ = 光の波長（nm）
R = リュードベリ（Rydberg）定数（ ≒ 1.097×10⁷m^-1）