ミンコフスキー空間

ミンコフスキー空間（Minkowski Spacetime）は、ドイツの数学者ミンコフスキーが考案した座標系です。特別な点は、座標系に空間だけでなく時間も含まれている点です。
ミンコフスキー空間は、数学の行列を使用して3次元空間と時間を統合し、4次元の座標系（x、y、z、ct）を表現します。しかし、4次元行列は非常に複雑であるため、通常は1軸（例：x軸）方向の運動だけを扱います。その場合、横軸は空間のx軸、縦軸は時間からなる座標平面（x、ct）になります。
ミンコフスキー空間を使うと、「双子のパラドックス」のような特殊相対性理論による「時間の伸び」現象を簡単に説明できます。

「双子のパラドックス」の投稿については、以下のリンクを参照してください。

双子のパラドックス

ミンコフスキー空間の理解

ミンコフスキー空間を導入するときは、次の点に注意してください。

観察者は、それぞれの座標系に基づいて周囲のものを観察します。
光の速度はどの座標系でも同じです。
光の速度が同じであるため、座標系の軸は曲がったり傾いたりすることがあります。

例えば、非常に速い（光速の半分）宇宙船が地球を出発して等速運動をしているとしましょう。

地球を基準に見ると？

青い帯は地球を基準とした時間帯です。
地球は静止しており、宇宙船は移動します。
移動中の宇宙船の時間は地球よりゆっくりと流れているので、伸びた時間だけ地球の時間帯から離れています。

地球と宇宙船の動きは、以下のようにミンコフスキー平面上の点で表示できます。

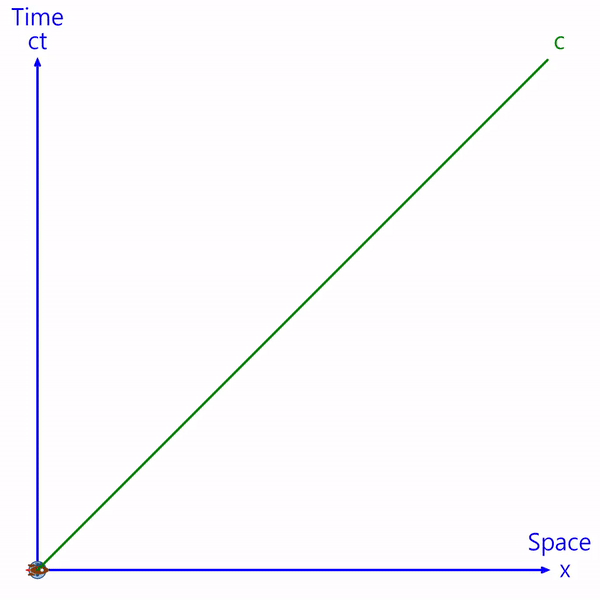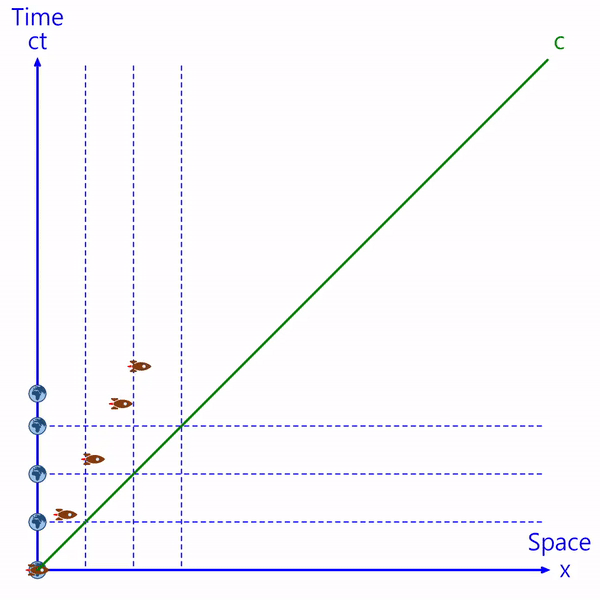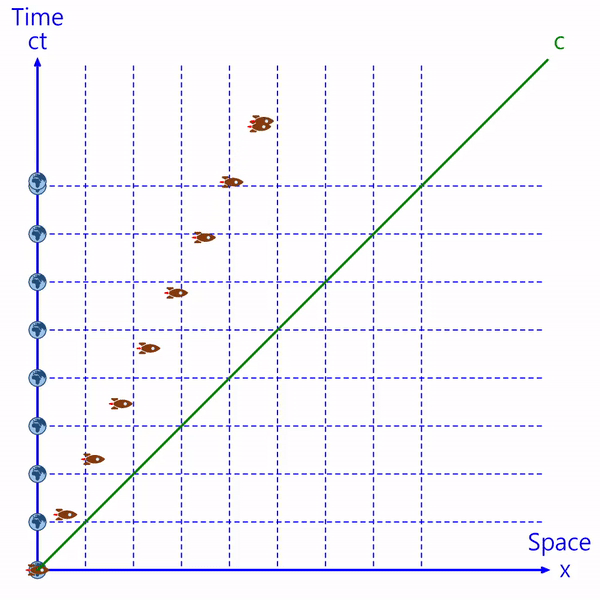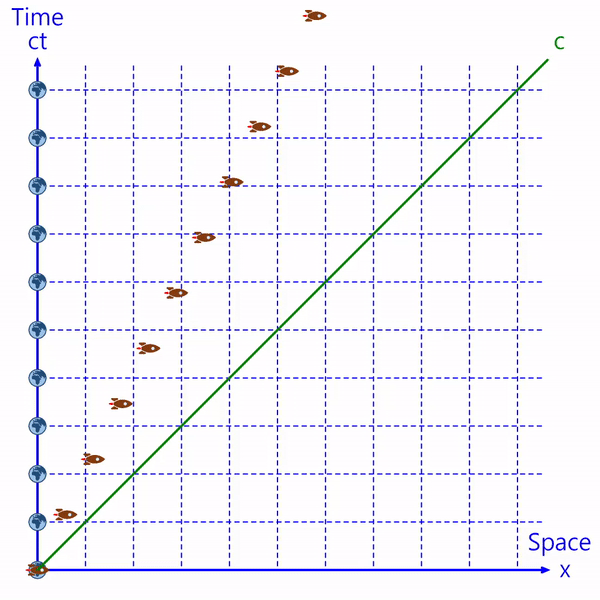
横軸は物体が位置する空間を表し、縦軸は物体の時間を表す。（縦軸は時間に光のスピードを掛けて「ct」で表示します。虚数を含めて「ict」で表示することもあります。）
地球を基準として考えると地球は停止しているので、地球は時間軸に位置します。
すべての物体のスピードは光より速くなることができないため、時空間上での宇宙船の位置は、光のスピード直線（c）より左側にあります。

宇宙船を基準にすれば？

宇宙船を基準とした座標系はどんな姿をしているのでしょうか？
宇宙船を基準とするというのは、位置が常に「0」という意味です。つまり、宇宙船は時間軸（ct '）の上にあります。

宇宙船を基準にすると、光のスピードはどのように変わりますか？
特殊相対性理論によれば、座標系が変化しても光のスピードは変化しない。言い換えれば、光束の傾き（c）は一定です。
時間軸(ct')が傾いた座標系で光束の傾きを一定に保つためには、空間軸(x')も傾けなければなりません。

したがって、宇宙船を基準とした時空間座標系は以下のように変形されます。（赤色）

2つの座標系を重ねてみると以下のようになります。

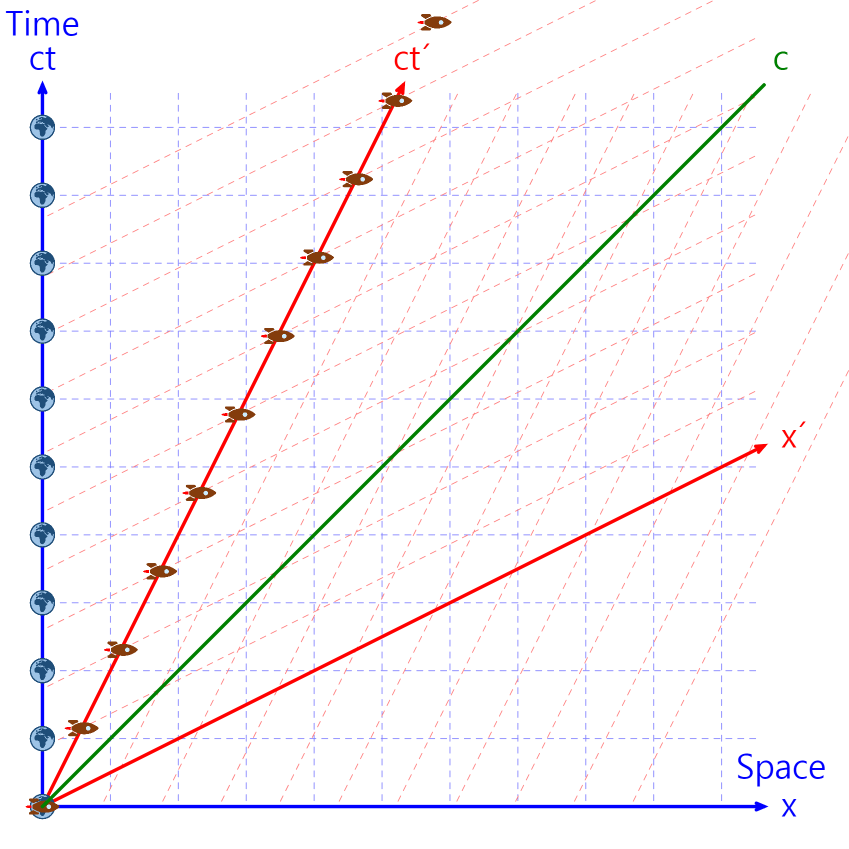
青い点線は地球を基準とした座標系、赤い点線は宇宙線を基準とした座標系です。
上のグラフは、次の現象を説明しています。

地球と宇宙船はそれぞれの座標系の時間軸の上にあります。つまり、停止している。
光のスピードは座標系に関係なくどこでも一定です。
地球と宇宙船はそれぞれ相手の時間がゆっくりと流れるように見える。

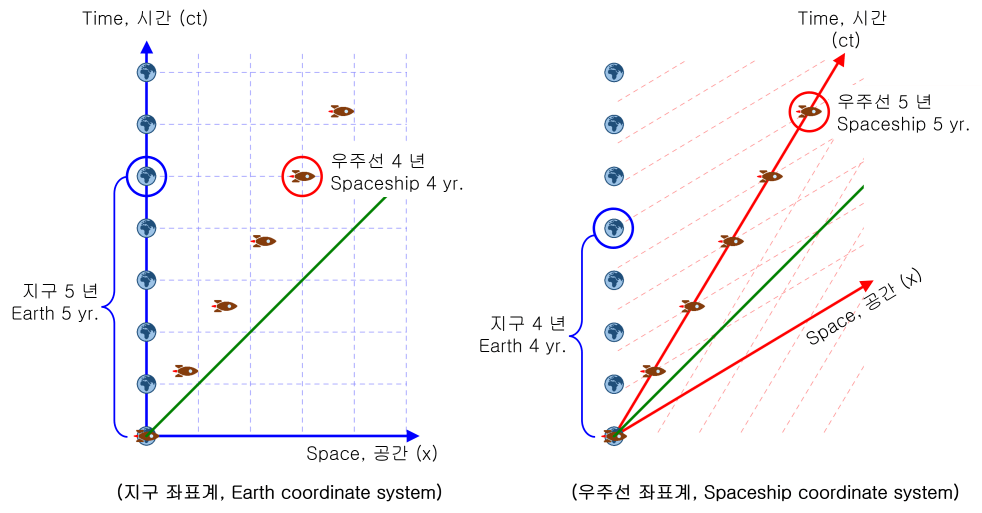
上の図は、宇宙船が光束の0.6倍で地球から離れることを示しています。 2つの図は互いに同じ動きであり、座標系だけが異なるように観察されたものです。
地球中心座標系で見ると、宇宙船の時間がゆっくりと流れています。
ところで、宇宙船中心座標系で見ると、地球の時間がゆっくりと流れているようです。
これは、それぞれの座標系で相手を観察するためです。