重力による張力
物理学では、張力は、二つの物体を接続したひもにかかる力です。一般的に、張力はひもの両端からひもの中心に向かうものと計算します。
長さが「\( l \)」である振り子を、「\( \theta_m \)」角度で持ち上げた場合を考えてみましょう。ひもの質量はないと想定します。
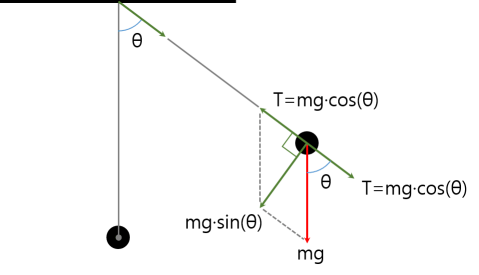
振り子に加わる力の源泉は、重力(=\( mg \))です。この重力は、次の二つの力で分解されます。
- 「重力による張力」 T = \( mg\cdot cos\theta \)
- 「重力によって振り子を動かす力」 = \( mg\cdot sin\theta \) (= T と mg のベクトル合計)
振り子の求心力
振り子が最高点から降りてくると、さらに一つの力が生じます。振り子の回転運動を維持するための求心力です。
振り子の長さが「\( l \)」であり、速度が「\( v \)」である場合、求心力は、次のとおりです。
\[ F=\frac{mv^2}{l} \]
求心力も、「重力による張力」と同様にひもの端から中心に向かいます。
ひもに加わるすべての張力
ひもに加わるすべての張力は、次のように計算することができます。
\[ \begin{align} すべての張力 &= 重力による張力 \, + \, 求心力 \\&= mg \cdot cos \theta \, + \, \frac{mv^2}{l} \end{align} \]
上記の式で、「\( v \)」と「\( l \)」を「\( \theta \)」に関連した式で簡単に作成します。
最高振幅が「\( \theta_m \)」であり、現在の振幅が「\( \theta \)」である振り子を考えてみます。
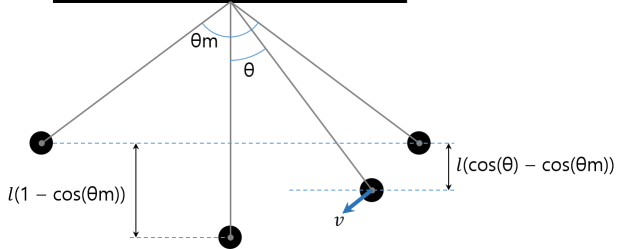
エネルギー保存の法則により、増加された運動エネルギーは減少された位置エネルギーと同じです。
\[ \frac{1}{2} mv^2 = mgl(cos \theta – cos \theta_m ) \\ \therefore v^2 = 2gl(cos \theta – cos \theta_m ) \]
上記の式を張力に代入してみると、
\[ \begin{align} すべての張力 &= 重力による張力 \, + \, 求心力 \\&= mg \cdot cos \theta \, + \, \frac{m \cdot 2gl(cos \theta – cos \theta_m )}{l} \\&= mg \cdot cos \theta \, + \, 2mg(cos \theta – cos \theta_m ) \\&= mg(3cos \theta – 2cos \theta_m ) \end{align} \]
になります。