定積分
2次元座標平面で定積分は、グラフの面積を求める方法です。
面積を横と縦の長さの積で簡単に入手できる場合は、唯一の長方形の場合です。
形状が一定しない場合、単純な乗算で面積を求めることができません。グラフの任意の区間が定められているとき、私たちはその区間の面積を求めるために、定積分を利用します。
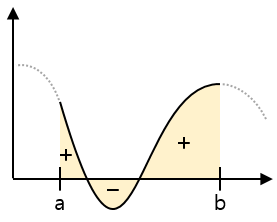
定積分の数学的な定義は次のとおりです。
区間の幅が限りなく小さくなるように区間を分割するとき、合計が常に一定の値に限りなく近くなると、その値を「f(x)」の「a」から「b」までの定積分で定義します。
\[ (面積) =\, \int_{a}^{b} f(x) \; dx \]
定積分する方法
積分をするには、まず微分を知る必要があります。
微分法については、各自検索してみてください。
積分は微分の逆関数と言うことができます。いくつかの関数「F(x)」をxについて微分した関数を、「f(x)」であると仮定しましょう。この場合には、「f(x)」を積分すると、「F(x)+ C(積分定数)」になります。
もし、関数式を積分することができれば、定積分の値は、次のように求めることができます。
\[ \int_{a}^{b} f(x) \; dx \, = \, F(b) – F(a) \]
物理学で頻繁に使用される定積分の事例
| 速度 – 時間グラフ |  |
面積 = 区間の時間の間に移動した距離
|
|---|---|---|
| 加速度 – 時間グラフ |  |
面積 = 区間の時間の間に速度が変化した程度
|
| 力 – 時間グラフ | 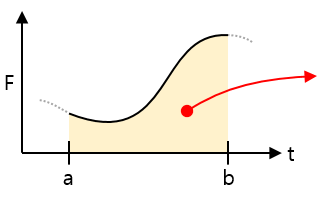 |
面積 = 区間の時間の間に受けた衝撃(運動量)
|
| 力 – 距離グラフ | 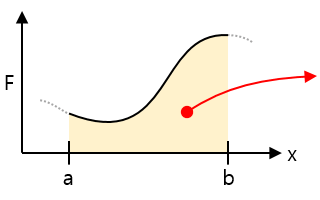 |
面積 = 区間の距離を移動するのにした仕事(W)の量、バネの場合バネに保存したり、解放されたエネルギー |