フーリエ級数
フーリエ級数は、一定の部分が繰り返される周期関数を単純な三角関数の和で表現する無限級数を指します。
単純な三角関数は、長い波のうねりのように滑らかな曲面で構成されています。これらの三角関数を続けて加えていくと一風変わった形の関数を得ることができます。
例えば、フーリエ級数を用いて長方形の関数を作ってみましょう。
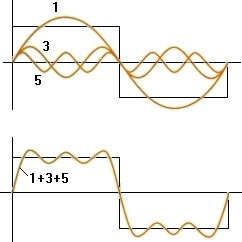
上図のように、通常の三角関数を3つ加えることで、四角形関数に近い形状を得ることができます。式で表示されてみると、次のとおりです。
\[ f(x)\, =\, sin(x)\, +\, \frac { 1 }{ 3 } sin(3x)\, +\, \frac { 1 }{ 5 } sin(5x) \]
今は3つの関数だけ加えたものなので、完全な正方形の形というには少し不足します。
しかし、このように無限に加えていくことができれば、最終的には、きれいな関数形を得ることができます。
\[ \begin{align}
f(x)\, &=\, sin(x)\, +\, \frac { 1 }{ 3 } sin(3x)\, +\, \frac { 1 }{ 5 } sin(5x)\, +\,… \\
&=\, \sum _{ n=0 }^{ \infty }{ \frac { 1 }{ (2n+1) } sin((2n+1)x) }
\end{align} \]
フーリエ級数の応用
フーリエ級数は、電子回路で、特定の波形を取得するのに主に使用されます。
例えば、方形波とのこぎり波のフーリエ級数式は次のとおりです。
